As easy as that

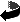
Once upon a time there was a triangle …

There is an infinity of tales on triangles. Or circles. Or conics. Some of them, though well known, I will try to tell once more, changing a word here and there.

  1. Center of gravity
  2. Bisector of an angle of a triangle
  3. ABC - 2250 years old problem
  4. Tangent and Ellipse
  5. Square

1. Center of gravity

As far as the center of gravity is concerned

(… the intersection of the medians …)
one may calculate a bit to see that it lies in two thirds of any of medians:

The calculation is:  [a+(a-v)] / v = v / (a-v) ,    so that     2 · a 2 = 3 · a · v  and     2 · a = 3 · v .

One can also realize it without really calculating, perhaps just counting the number of equal segments:

2. Bisector of an angle of a triangle

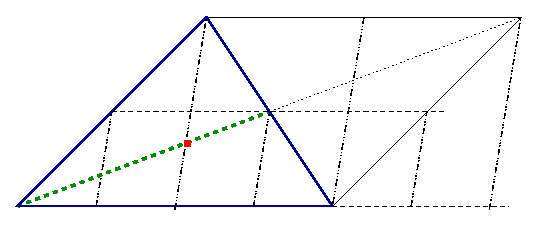
The bisector of an angle between two sides of a triangle divides the third side into segments proportional to the sides that meet them in the vertices of the triangle.

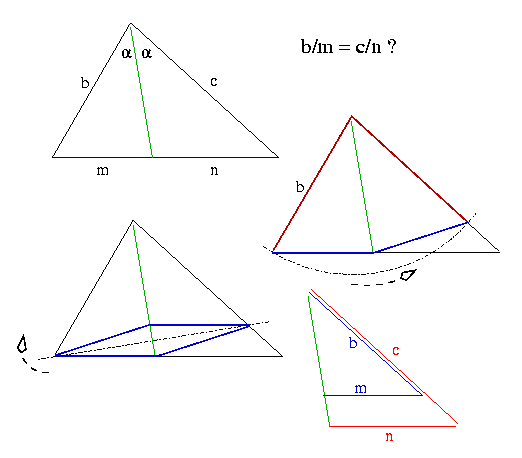
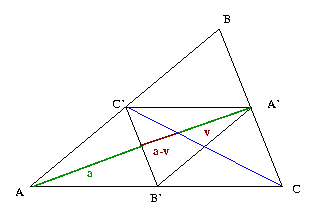
Perhaps you prefer another proof? If you produce a paper model with two copies of the triangle on the left glued one on top of the other along the bisector - and make a necessary incision in the lower part of the bisector than you can make a visual demonstration performing two consecutive paper foldings.

3.   ABC - 2250 years old problem

Finding the midpoint of an interval is the most elementary construction, right?



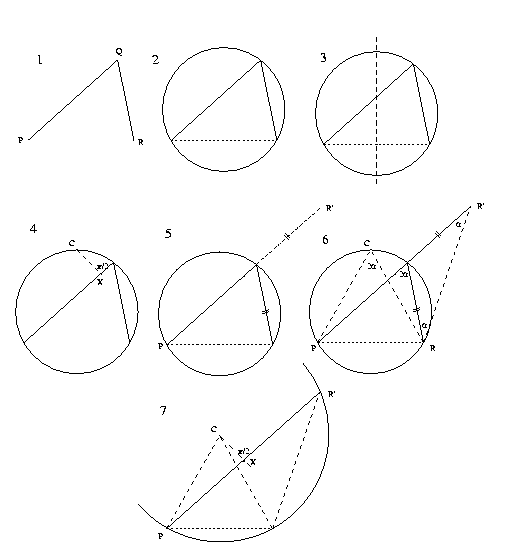
Archimedes' Broken Chord? Well, where does this name come from?

All this story is told in one picture on the very first page of Episodes in Nineteenth and Twentieth Centure Euclidean Geometry by Ross Honsberger (AMS, NML, Washington 1995) - what is the point in repeating it?

Well, it is just seven points, not a point. Bytes are cheaper than paper and I can afford to make a story somewhat longer. I get confused when the same sketch transmits many different arguments at the same time.

4.   Tangent and Ellipse

Given a point on the ellipse, how to trace a tangent line? Well, perhaps we had better ask first: what does it mean? No derivatives are permitted; the same goes for coordinates, we are talking about geometry. And for many centuries before Descartes and Newton human beings managed to work with lines tangent to ellipses. Was it terribly difficult?

Perhaps not. Just take a look at four pictures below. The first of them introduces the notions. Two others show how to construct the tangent. The last one should convince you that the constructed line catches the ellipse in only one point.

5.   Square

The exercise appears in our (Waldir Quand & A.S.) collection (ex.15) and we thought that we had invented it. Well, what I mean is that we did not borrow it from any other collection. One has to calculate the area of the red square:

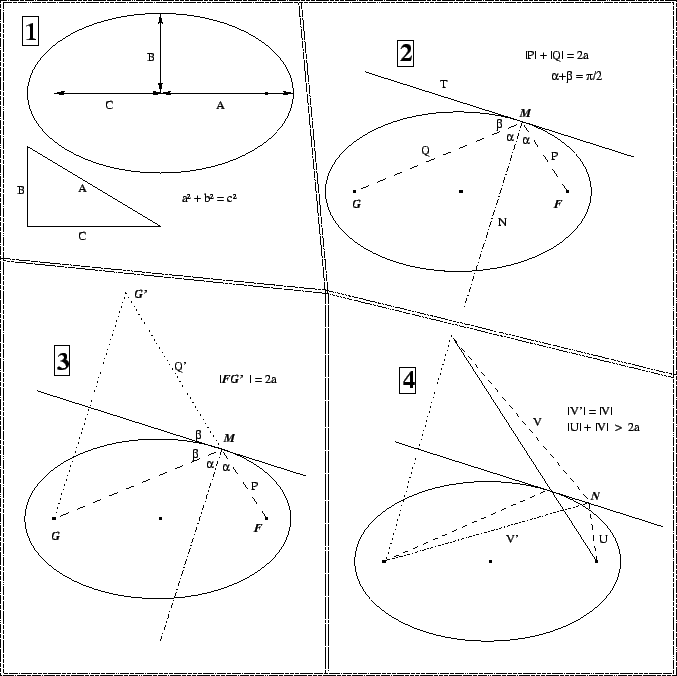
A part of its charm stems from the fact that there are really many ways to approach it. I used to suggest to my students that this solution

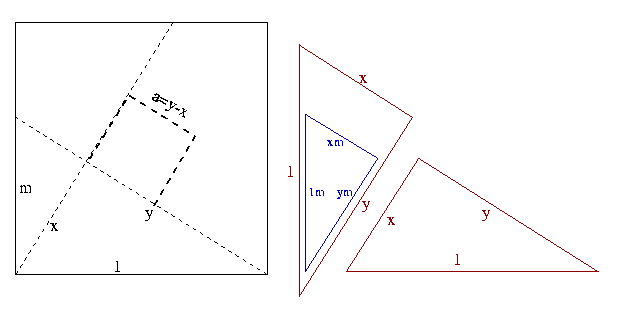
asked for a minimum of calculations: as x=ym, you use the Thales theorem to get a=y(1-m), then Pythagorean theorem gives you  y2(m2+1)=1 and the final result

a2 = [(1-m)2] / (m2+1)
is ready.

One day I realized that I have already seen a nice solution for the specific case of m=1/2; it appeared in one of the first issues of Revista do Professor de Matemática in the early eighties. The solution was attributed to Raul Neder Porrelli:

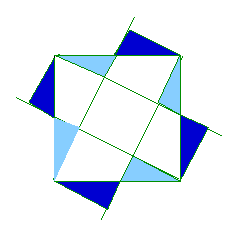
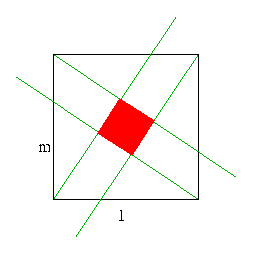
Exchanging light-blue triangles for dark-blue ones you see that there are 5 small squares in the big one.

Some more years passes and something led me to apply to myself the advice that I always offer to my students (even if they do not ask for it): revisit the old solutions, ask yourself why it worked. 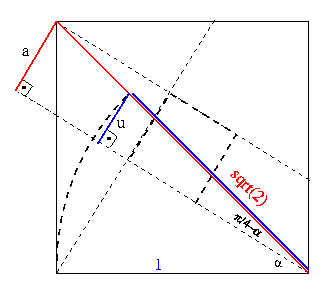So I thought: the formula for a looks like a tangent of a difference of some angles, why not to try it once more - after all I know the angle if the value of the function tan is 1 … Yes, the obsevation resulted in another, much shorter, proof: if you name the angle and give some cosmetic touches

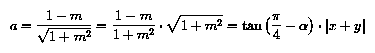
the you get something that is easier to visualize

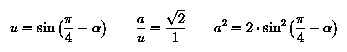
and the new proof is ready to enter:

Obviously, I liked and I was ready to say it good-bye but then unexpectedly I met two articles on the Internet dealing with the very square: this one and one more. What a surprise … perhaps it is too early to say goodbye to my little friend?

Added on Nov. 4, '01

My friend writes me:

If you discard the prolongation of half-lines that stick beyond the small square then you get the figure of Bhaskara's proof of Pythagorean theorem. (Sure. Shame on us not to note it.) By the way, the square appears also in nature.
It does in fact - and the internal divisions are nicely used to point to different directories of the site:

Added on Feb. 5, '02.

In order to have an encounter with the most recent offspring of this family of figures have a look at Crux Mathematicorum with Mathematical Mayhem, vol.27 (6, October 2001), p.391. The Mayhem staff proposes that the area of the small square is 1/2001 and asks what is m.

Moving in the other direction in time one finds the article “A Round-Up of Square Problem” by Duane Detemple and Sonia Harold in Mathematics Magazine, vol.69 (1, February 1996), p.15-27; in its turn it directs the reader to the article “Dörrie Tiles and Related Miniatures” by Edward Kitchen in Mathematics Magazine, vol.67 (2, April 1994), p.128-130; the case of m=1/2 solved just as I have found it in RPM stands there - but attributed to Heinrich Dörrie; the reference sends to his book Mathematische Miniaturen published in Breslau in 1943.