Dodawanie i mnożenie punktów

Zazwyczaj uczymy się wykonywać operacje arytmetyczne (dodawanie, odejmowanie, mnożenie, dzielenie) używając punktów linii prostej. Nazywamy ją „prostą rzeczywistą” i mówimy o „liczbach rzeczywistych”. Może dlatego inne podejścia do arytmetyki nie wydają się rzeczywiste i otrzymują odstraszające nazwy. W rachunkach wykorzystujących punkty płaszczyzny daje się tym punktom nazwę „liczb”, ale z przymiotnikiem „zespolone” – a co gorsza, niektóre z tych zespolonych doczekały się epitetu „urojonych”.

Gdyby liczby były towarami, to reklama przysporzona taką nazwą zagwarantowałaby ich wieczną niesprzedawalność.

Kto cierpliwie przeczyta moje uwagi aż do końca może dojdzie do zaskakującego wniosku, że działania na owych „liczbach zespolonych” tworzy się dużo naturalniej niż w przypadku liczb „rzeczywistych”, czyli mogą być różne „normalności”. Ale to, co tu opowiem, nie jest próbą rewolucyjnego wywrócenia do góry nogami pojęć o liczbach. Matematycy wiedzą o tym wszystkim doskonale (a przynajmniej powinni wiedzieć) i jeśli w swoich książkach nie wprowadzają w ten sposób arytmetyki liczb zespolonych to muszą ku temu mieć jakieś ważne powody.

Ktoś mi mówił, że Roger Penrose tak wprowadza liczby zespolone w jednej ze swoich książek.
(Dopisek z października 2006)
Przy okazji: nie mam pojęcia jakie to mogą być powody i gdyby to ktoś odkrył, uprzejmie proszę o pilne powiadomienie mnie.

Prosta liczbowa

Zacznijmy od linii prostej, choćby dla przypomnienia pojęć. Z dodawaniem i odejmowaniem jej punktów nie ma kłopotów. Trzeba wybrać punkt zaczepienia czyli 0 („zero” to nazwa a nie prawo natury) i punkty a,b traktujemy jako strzałki („wektory”) zaczynające się w zerze, kończące się w owych punktach. Dodawanie to zestawianie ich stawiając początek drugiej strzałki na końcu pierwszej. Punkt, w którym skończyła się przestawiona druga strzałka nazywamy sumą a+b. Jeśli umówimy się, że -a to punkt tak odległy od zera jak a lecz „z drugiej strony zera” (nazwiemy go liczbą przeciwną do a) to odejmowanie liczb a-b wprowadzamy za pomocą dodawania:

a-b = a + (-b)

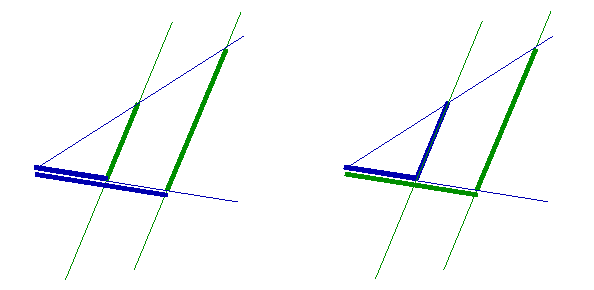
„Geometryczne” mnożenie punktów prostej ma długą historię. Można ją zacząć od „twierdzenia Talesa”. O Talesie z Miletu wiemy, że istniał i być może wymyślił swoje twierdzenie. Ktoś z pewnością je wymyślił, więc czemu by nie nazywać go, jak to inni czynią, twierdzeniem Talesa.

Jego treść w gruncie rzeczy jest taka: oglądając płaszczyznę z daleka i z bliska widzimy odmiennie figury – ale stosunki między długościami ich części nie zmienią się. Możemy wyobrazić to sobie myśląc o oglądaniu figury „normalnie”, a potem przez lupę, ale bez zniekształceń.

Ale Tales nie miał lupy, a nieprecyzyjne wyrażenie „brak zniekształceń” może doprowadzić do nieporozumień. Pomysłowe pozbycie się tej trudności polega na przyjęciu, że jeśli przekształcamy płaszczyznę, to linie proste pozostają liniami prostymi, kąty nie zmieniają się a pary linii równoległych nadal będą równoległymi. Na ogół przedstawia się to takim rysunkiem:

używając wyjaśnienia: stosunek między pogrubionymi zielonymi odcinkami jest ten sam co między pogrubionymi niebieskimi odcinkami. (Wszystko jedno czy myślimy o szkicu po lewej czy po prawej stronie, bo jeśli a/b=c/d, to także a/c=b/d.)

René Descartes wykorzystał ten pomysł tworząc „geometrię analityczną”. Nastąpiło to dużo później, mniej więcej 2300 (słownie: dwa tysiące trzysta) lat po wymyśleniu twierdzenia Talesa. Wbrew rozpowszechnionym przekonaniom, nie stworzył nowej geometrii wprowadzając współrzędne punktów na płaszczyźnie i w przestrzeni, bo to wymyślił z 1500 lat wcześniej Ptolomeusz z Aleksandrii. Zasługą Descartesa było pokazanie, że mając dwa odcinki (oraz odcinek, służący za jednostkę), dzięki twierdzeniu Talesa można konstruować iloczyn i iloraz tych liczb. Zacznijmy od iloczynu. Mając a,b i 1, buduje się x=ab – ale trzeba wyjść poza prostą zawierającą te odcinki. To znaczy, że geometryczna konstrukcja iloczynu liczb rzeczywistych nie jest wykonywana na prostej rzeczywistej.

Odcinek mierzący a musi być oparty na prostej tam, gdzie kończy się 1. Jego kierunek jest obojętny, pod warunkiem, że nie zbiega się z kierunkiem tej prostej!

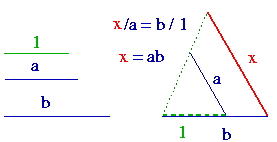
Dzielenie nie wymaga nowego obrazka, bo przepis jest oczywisty: dzielenie a/b jest mnożeniem ab^-1, więc wystarczy skonstruować liczbę b^-1. Jeśli mam 1 oraz b, to x=b^-1 dostanę z proporcji x/1 = 1/b.

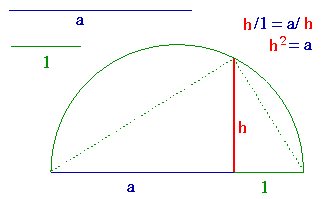
W owym cyklu odkryć Kartezjusza ważne też było stwierdzenie, że wykorzystując podobieństwo trójkątów (czyli twierdzenie Talesa) można skonstruować kwadratowy pierwiastek z liczby a. Widać to na poniższym szkicu, spożytkowawszy dość oczywisty fakt, że kąt oparty na średnicy okręgu jest prosty.

Płaszczyzna liczbowa

Historycy znajdują elementy rachunków wektorowych już w traktatach starożytnej Grecji. Trudno by było więc przypisać te pomysły jednej konkretnej osobie i z pewnością nie był wynalazcą tego narzędzia Isaac Newton. Ale jego niesłychanie wpływowe Matematyczne zasady naturalnej filozofii, wydane w roku 1686, przedstawiły ideę równoległoboku sumy sił już na początku książki (we wstępnej części Aksjomaty, czyli prawa ruchu) i język jest prawie współczesny nam, a choć dodanie wektora i jemu przeciwnego nie jest narysowane, „Prawo III” to stwierdzenie, że dla każdej „akcji” (czyli działania siły) istnieje równa jej w wielkości lecz przeciwna w działaniu „reakcja”.
Dziś w modzie jest wprowadzenie tych pojęć bez odwoływania się do znaczenia fizycznego, czyli wybieramy trzy punkty na płaszczyźnie, tworzące dwie liczby (jeden punkt służy za 0) i dodajemy oraz odejmujemy liczby z,w zgodnie z tym szkicem:

Co robić jeśli trzy punkty leżą na jednej prostej? To świetne ćwiczenie, które rozwiąże każdy, kto przeczytał pierwszą część tego tekstu.

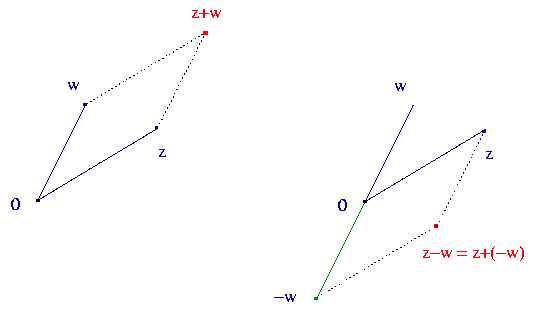
Równie dobrym ćwiczeniem jest przedstawienie sobie znaczenia geometrycznego praw przemienności i łączności dodawania: dla wszelkich z, w, u z płaszczyzny zachodzi

z + w = w + z ,

(z + w) + u = z + (w + u) .

To są aksjomaty. Uwidocznienie ich sensu nie służy dowodzeniu ich, bo aksjomaty przyjmuje się bez dowodu, lecz pojmowaniu skąd się wzięły i do czego służą. Powtórzmy słowami to, co te symbole mówią. W pierwszej linii mamy dwa składniki, a w drugiej – dwa działania. Prawo przemienności ustala, że wynik nie zależy od kolejności użycia dwóch składników. Prawo łączności ustala, że wynik nie zależy od kolejności wykonania dwóch działań.

Minęło kolejnych 120 lat nim pewne dziwne rachunki objawiły swoje znaczenie geometryczne jako mnożenie na płaszczyźnie. Nie ma potrzeby przebiec wraz z wynalazcami z XIX wieku całej trudnej drogi do sukcesu, dziś jest on łatwo dostępny jeśli użyjemy takiego podejścia:

Jeśli mam cztery punkty 0, 1, z, w, które nie leżą na jednej prostej, punkt zw (iloczyn z i w ) wprowadzam przez żądanie, że dwa trójkąty o wierzchołkach
0, 1, z
oraz
0, w, zw, są podobne i mają tę samą orientację na płaszczyźnie.

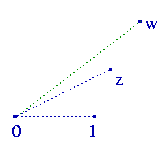
Ten drugi trójkąt ma trzy wierzchołki „przemnożone” przez w, więc można wyobrazić sobie, że jeśli odcinek od 0 do 1 jest podstawą pierwszego trójkąta, drugi ma za podstawę odcinek od 0 do w. Dlatego stosunek podobieństwa dwóch trójkątów ma wynosić |w| : 1.

Jak go skonstruować? Obróć trójkąt (0,1,z) tak, by oparł się na półprostej zaczynającej się w 0, skierowanej ku w, po czym rozciągnij (czy też skurcz) go tak, by jego nową podstawą był odcinek od 0 do w.

Szkice ujawniły dwie kluczowe własności tego mnożenia: kąty dodaje się, długości („moduły”) mnoży się.

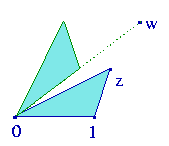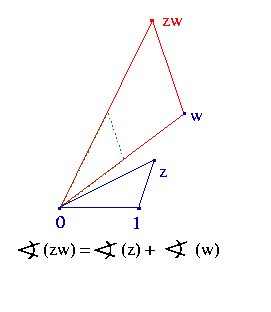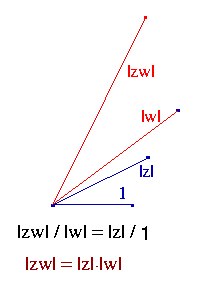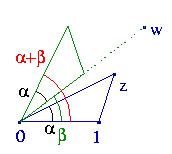
Ćwiczenie: jaki jest kąt iloczynu, jeśli suma kątów przekroczyła pełen obrót? Oczywiście kąty mają kierunek, idą przeciwnie do wskazówek dawnych zegarów.

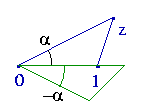
Niemiła niespodzianka z nazewnictwem: nie mówi się o kącie między odcinkami 01 oraz 0z, ale o „argumencie liczby z”, zapisanym jako Arg(z). Tak więc musimy pisać

Arg(zw) = Arg(z) + Arg(w) 
albo wywoływać burzę w szklance wody wprowadzając sensowniejsze lecz nieznane powszechnie nazwy.

Kolejny szkic pokazuje, że i dzielenie na płaszczyźnie jest elementarną sprawą:

bowiem trójkąt z wierzchołkami 0, 1/z, 1 jest podobny do trójkąta z wierzchołkami 0, 1, z (przemnożyliśmy je przez z^-1). Jak uprzednio, umiejąc znaleźć liczbę odwrotną do z, umiemy dzielić przez z.

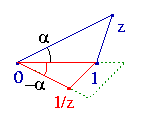(Jeszcze jedno ćwiczenie: czy jest jakaś liczba na płaszczyźnie, przez którą nie da się dzielić innych?)

Wierzę, że sporządzenie szkiców ilustrujących przemienność i łączność mnożenia nie stanowiłoby ćwiczenia przesadnie nużącego czytelnika. Kto woli mechaniczne podstawy dla swoich przekonań, może oprzeć zaufanie do tych praw na sprowadzeniu opisu mnożenia punktów do dodawania kątów i mnożenia długości odcinków.

Nieco bardziej skomplikowane jest uwierzenie w prawo rozdzielności (mnożenia względem dodawania):

a(b + c) = ab + ac .

Gdy chodzi o liczby rzeczywiste, prosty szkic wydaje się przybliżyć sens tej tożsamości:

Bywają takie osoby, co czepiają się szczegółów i twierdzą, że to nie ma sensu. Niestety mają one rację. Po lewej stronie dodajemy miary obszarów (pola prostokątów), a po prawej – miary odcinków. Więc ten sam znaczek „+” ma na rysunku dwa różne znaczenia, a w tożsamości powinien znaczyć zawsze to samo. (W istocie, to jest ilustracja tego jak definiuje się miarę figur.) Mamy tu odległy ślad kłopotu pojęciowego starożytnych Greków, którzy traktowali iloczyn jako miarę pola (prostokąta) a liczbę jako wymiar odcinka (ściślej mówiąc: stosunek jego długości do długości wzorcowego odcinka zwanego „jednostką”). To rozdwojenie musiało przynosić konflikty, bo trudno taki rozdział pogodzić na przykład z równością 15 = 3·5 – czy w niej obie strony są czy nie są tym samym?

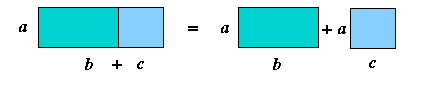
Pewna doza cierpliwości pozwala przedstawić tę samą zasadę zastosowaną do liczb z płaszczyzny jako stwierdzenie, że obrócenie błękitnego trójkąta o Arg(z) i rozciągnięcie go o |z| (przemnożenie liczb 0, w, u + w przez z) przenosi jeden z jego wierzchołków do punktu zu + zw.

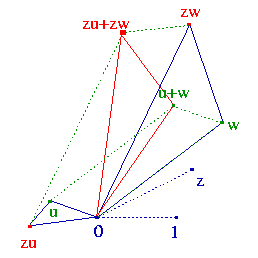Dopiero teraz docieramy do niepokojącego zazwyczaj równania: √-1 = i . Na prostej prostopadłej do odcinka 01 symbolem i oznaczę punkt odległy od zera o 1 i leżący „nad zerem” (gdybym wybrał taki punkt „pod zerem”, zmieniłaby się jedynie orientacja płaszczyzny, czyli kąty byłyby mierzone tak jak nakazują wskazówki dawnych zegarków).

Podniesienie i do kwadratu daje w wyniku punkt wyznaczony kątem równym dwóm kątom prostym i mający moduł równy 1·1 = 1 . Ale ten punkt jest przeciwny do 1, więc i ² = -1 .

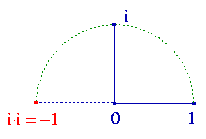
Szkolna prawda „nie ma pierwiastka kwadratowego z liczby -1”  przestała być prawdziwa. Nie ma go na prostej zawierającej 0 i 1 – ale jest gdzie indziej.

Jak powiązać to wprowadzenie do liczb zespolonych z „normalnym”? Zapisując punkty płaszczyzny we współrzędnych, otrzymanych dzięki liczbom 1 oraz i. Powiedzmy, że do punktu z docieram poruszając się w prawo (lub w lewo) odcinkiem a1, a potem do góry (albo do dołu) odcinkiem bi. To znaczy, że zamiast myśleć o parze współrzędnych (a,b) mogę wziąć liczbę z = a+bi (konwencja dopuszczająca a=a1 upraszcza zapis). Przedstawiam też w podobnej formie w = c+di, wykorzystuję rozdzielność oraz łączność i przemienność obu działań, dostaję algebraiczne wzory, od których zazwyczaj zaczyna się wprowadzenie do liczb zespolonych.

I jeśli nie chcę, nie muszę więcej robić szkiców, bo geometria jest przetłumaczona na sprawne i zwięzłe formułki. I to ile ich! Obroty na płaszczyźnie, odbicie w jakiejś prostej, przesunięcia (czyli translacje), wzory trygonometryczne, klasyczne twierdzenia geometrii – wszystko to opisuje się w tym języku, lecz używając o połowę mniej stron. To nie przypadek, że nauki inżynierskie przyspieszyły swój rozwój i uprościły opis po przyswojeniu sobie języka liczb zespolonych w stopniu porównywalnym z tym, co nastąpiło gdy wykorzystały wynalazek rachunku różniczkowego i całkowego.

Epilog

Mam nadzieję, że nie wyjdę na zabytek historyczny wygłaszając tu taki apel: drodzy, do cyrkla i linijki! Multum ciekawych odkryć czeka na was.

Nie brzmi to tak atrakcyjnie jak zachęta do nowego typu komputera, a odkrycia, które robi się tu zostały już porobione, niektóre z nich przed dwustu laty, a inne przed dwoma tysiącami lat. Ale zostawienie na uboczu gier komputerowych i zabawienie się w odkrywcę prawd geometrycznych przy użyciu liczb zespolonych może przynieść zadziwienie swoimi własnymi talentami.

Wierzę, że to jest ważne. Wprawdzie nie szło tam o liczby zespolone, ale to dzięki takiemu nastawieniu stworzono najpotężniejsze na świecie społeczeństwo. To kwestia zaufania do prostego i krótkiego wezwania:

Zrób to sam.