QUAL É MESMO A CONTRIBUIÇÃO DE DESCARTES?

Há uma convicção generalizada que o sistema de coordenadas foi introduzido no século XVII pelo Descartes. Mesmo que a constatação não é falsa, tem muitos desentendimentos acerca dela e perderia seu tempo aquele que procurasse em sua La géométrie de 1637 qualquer desenho de eixos $ Ox$ e $ Oy$. (A idéia de descrever um ponto no espaço dando suas três coordenadas ocorreu já aos matemáticos gregos em sec.III a.C. – Ptolomeu usava o recurso sistematicamente na descrição de posição de estrelas...) Em que, então, consistiu a atitude revolucionária de tratamento dado pelo Descartes a geometria – e qual é a ligação disso com o teorema de Tales? Para responder a esta pergunta talvez vale a pena ler a famosa “La géométrie” de Descartes – ou pelo menos o início dela. Para facilitar o trabalho coloco-o adaptado à linguagem de hoje. Não posso chamar as seguintes linhas de uma “tradução”; quis obter a fidelidade ao sentido e não ao verbo. Note que o texto foi escrito há 360 anos, desde então havia mudanças tanto em sentido de termos específicos quanto no modo de compor as frases ou conduzir os argumentos.

Problemas com construção

exigindo apenas retas e círculos.

Qualquer construção geométrica pode ser descrita desse modo que o conhecimento de comprimentos de certos intervalos já leva a execução dela. Assim como a aritmética consiste de quatro ou cinco operações (quer dizer: adição, subtração, multiplicação, divisão e extração de raízes – e esta operação pode ser vista como uma espécie de divisão), também em geometria para achar intervalos desejados precisa-se apenas adicionar ou subtrair outros intervalos – ou usar uma das operações seguintes: tomando um intervalo escolhido a vontade chamo-o de unidade (e faço isso para sugerir maior possível semelhança com os números) e tendo dois outros intervalos busco o quarto que será tão relacionado com um deles como o outro com a unidade (e esse processo seria o mesmo que a multiplicação). Depois (para aqueles dois intervalos) busco o quarto que tem-se a um deles como a unidade ao outro (e esta vez teria a divisão). Finalmente, busco uma ou algumas médias entre a unidade e um dado intervalo (e agora teria a extração de raiz quadrada, cúbica etc). E não hesitarei de introduzir esses termos aritméticos para a geometria em nome de maior clareza.

Não sou adepto de “embelezamento histórico” de textos matemáticos. Se um livro de geometria analítica menciona que “coordenadas cartesianas foram introduzidas por Descartes” e coloca uma ilustração do dito cujo (sequer explicando o grau de confiabilidade dela) mas nem toca no assunto de sentido dessa frase sobre “introdução”, os estudantes estão levados mais em direção do preconceito do que de conhecimento. Surge uma convicção que antes do Descartes ninguém entenderia a frase do tipo “vá 100 passos em direções daquela árvore e depois 25 passos para direita”. Mas … será que o Colombo não usava os mapas? Ou só depois de Descartes foram inventadas as direções de leste-oeste e norte-sul? Obviamente há algum ponto mais fino nesta estória.

Bem, desde os tempos de Tales sabia-se que a única interpretação geométrica do produto de dois comprimentos é uma área do retângulo com as adequadas arestas. Foi uma grata surpresa quando com a frase citada acima Descartes sugeriu a receita: “pegue os intervalos com comprimentos $ 1,a,b$, ajeite-os como mandam as hipóteses do teorema de Tales para que o seu esboço corresponda à proporção $ \, \frac{a}{1}=\frac{x}{b}\,$, o quarto intervalo que surge da construção tem justamente o comprimento $ x=a\cdot b$.” É surpreendente que durante 2300 anos1 ninguém se deu conta das possibilidades que oferecia o teorema de Tales – mesmo que esse resultado fazia parte indispensável da instrução.

A conseqüência da invenção não era a capacidade de marcar no plano um ponto designado por dois números – digamos 5 e 7 – que corresponderiam às quantias adequadas de certas unidades, traçadas em duas direções – mas a capacidade de marcar pontos descritos por duas expressões envolvendo variáveis e operações aritméticas! O trabalho de Vieta em décadas anteriores consolidou o uso de símbolos gráficos para constantes e variáveis2 – mas agora a capacidade de construir um ponto designado – por exemplo – por $ x$ e $ x^2$ abria o caminho de duas vias entre a geometria e a aritmética. Portanto a revolução cartesiana apoiava-se em criação da reta numérica. Ou talvez semi-reta, pois a interpretação de “números negativos” como pontos da reta surgiu uns trinta anos mais tarde como efeito de estudos da obra de Descartes, estudos feitos por Isaac Newton.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

... anos1
Sabia-se há tempo que também um tal de Bombelli no século XVI percebeu isso – a descrição dele foi achada no manuscrito e publicada neste século. Alguns anos atrás os historiadores da ciência descobriram que Bombelli já divulgou essa descrição no seu livro “Álgebra” publicado ainda em 1572. Portanto, a rigor, o trabalho do Descartes não era em 100% original e inédito – mas foi primeiro que teve uma significativa divulgação e influência social.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

... e variáveis2
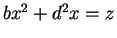Uma citação curta mas ilustrativa da escrita de Vieta do final de século XVI: B in A quadratum plus D plano in A aequari Z solido. – com vogais designando variáveis e consoantes designando constantes (dados); hoje isso seria escrito como $ bx^{2}+d^{2}x=z$.