Das duas técnicas que mecanizam a multiplicação: deslocando as “casinhas” e a geloxia, ganhou a pior. A outra teve de perder por um motivo inaparente, a necessidade de traçar linhas transversais. Isso era uma dificuldade considerável na época quando imprensa usava as fontes móveis. As linhas horizontais e verticais eram mais em consonância com a tecnologia. Vi na Rede que por volta do novembro de 2006 a geloxia fez uma entrada triunfal, aparecendo sob o disfarce de “multiplicação por desenho”. Alguma página estava expondo isso com nome de “Easy Graphical Multiplication Trick” (“um macête fácil de multiplicação gráfica”), outro fala: “Math Lesson: A new way to multiply” (“aula de matemática: o novo método de multiplicar”). Ambos os títulos revelam um desentendimento. Não é um macête mas sólida e bem conhecida multiplicação, descrita em uma outra maneira. E quanto à novidade, vê que este esboço exemplifica o método – e apareceu em primeiro livro que foi impresso e versava sobre aritmética; o ano da produção é 1478, o lugar é Treviso na Itália mas o autor é desconhecido.

Isto é um empréstimo da pag.99 de “A History of Mathematical
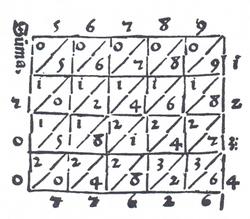
Notations” de Florian Cajori, Dover 1993.)

Vou começar de caixinhas que aparecem na tabuada, mas desenhando-as de outro modo.

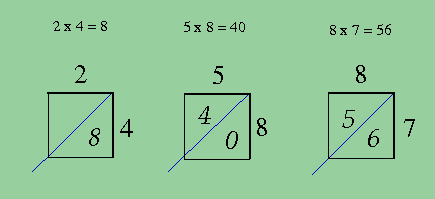
Quando multiplico dois números que tenham um algarismo e o resultado também não ultrapassa 9, escrevo-o no triângulo de baixo. Se o resultado tem dois algarismos, o primeiro vai para o triângulo superior, o segundo para inferior.

Espero que você distingue algarismos e números. Caso há problemas, lembro: letras descrevem palavras, e algarismos descrevem números. Podem acontecer dúvidas, pois há palavras de uma letra e há números de um algarismo, mas do texto, do ambiente onde o sinal gráfico aparece deve ficar claro se temos um algarismo (uma notação) ou um número (um bicho que pertence à fauna matemática).

Quando quero multiplicar dois números com vários algarismos, o primeiro número anoto em linha acima dos quadradinhos, o segundo – na vertical à direita dos quadradinhos; em cada dos quadradinhos anoto o resultado de multiplicação dos números correspondentes que tenham um algarismo.

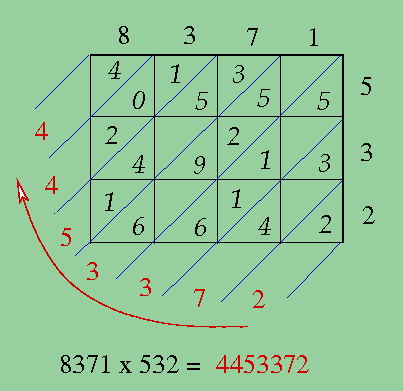
Depois (da direita à esquerda) junto números de faixas demarcadas por linhas diagonais em azul. Se a soma ultrapassa 9, anoto só o último algarismo do resultado em baixo em vermelho, o resto adiciono aos números da próxima faixa à esquerda. Acabou.

Vários especialistas concordam que este processo é mais fácil explicar para uma criança do que a multiplicação escolar (com um “empurrão” à esquerda. Mas, como falei, a decisão foi tomada pelas editoras: as linhas transversais exigiriam muito trabalho. Você precisaria de fontes para todos os números de 0 até 99 em quadrados cortados pelas diagonais.

A situação lembra as lutas entre o uso de VHS e Betamax para filmes. O melhor perdeu, só os cineastas usavam Betamax – e ambos os sistemas estão caindo em esquecimento por causa da notação digital dos filmes, como arquivos eletrônicos. As crianças nas escolas aprendem a notação de multiplicação em várias linhas, mas isto é uma hipocrisia, pois os adultos usam nesses casos calculadoras.

Não estou dizendo que a idéia simpática da geloxia foi disperdiçada. As idéias têm mais vidas do que os gatos. Mas em suas consecutivas reincarnações as idéias escolhem corpos diferentes. No início do século XIX William George Horner elaborava uma técnica de cálulo de valores de polinômios e as vezes os dividia. De fato, usava algo muito parecido com o algoritmo de Euclides. Desses esforços dele preservou-se um produto secundário em forma de técnica com sólido valor didático, chamada de “esquema de Horner de multiplicação de polinômios”:

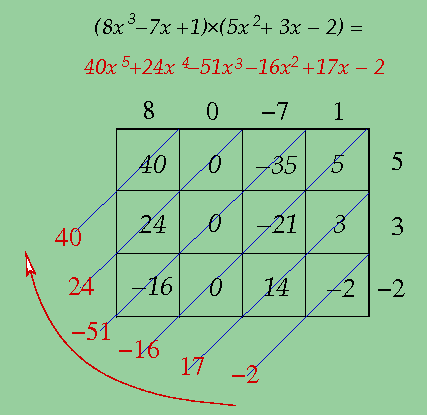
Se quer achar coeficientes de produto de dois polinômios, coloque todos os coeficientes do primeiro (todos significa: mesmo os “invisíveis”, com 0 ou 1) horizontalmente acima dos quadrados, de mais alto até o último, coeficiente livre, depois faça o mesmo com o outro polinômio verticalmente; em baixo junte ao longo das diagonais os números que aparecer junto aos expoentes iguais e o resultado anote em forma polinomial.

Na prática, os polinômios também são multiplicados com freqüência cada vez maior por computadores: abro o programa pari-gp – ele me economiza tempo e salva de muitos erros calculacionais (esquecimento de sinais e parecidos). Mas as vezes tem de multiplicar...

Divertido: há tempo isso foi ensinado na escola de segundo grau. E recentemente apareceu um artigo de um bom pedagogo (Jeff Suzuki) em uma decente revista de matemática mais ou menos elementar, The College Mathematics Journal (janeiro 1999, pag.50-53). O título: Multiplying and Dividing Polynomials Using Geloxia. Se as coisas correrem desse jeito, revistas matemáticas vão divulgar a tabuada...

Quem conhece matrizes e não quer multiplica-las no computador, pode usar uma idéia com esquema bem parecido. Se matriz A tem o mesmo número de colunas que tem linhas na matriz B, podemos coloca-las desse jeito:

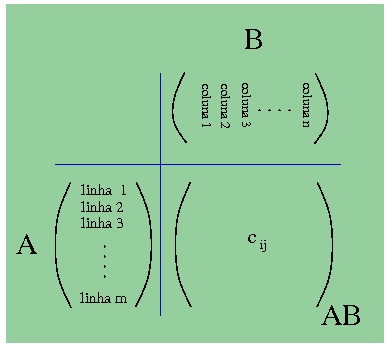
e lá c_ij é o produto da i-ésima linha de A com j-ésima coluna de B.

O leitor que porventura chegar ao original desta nota em meu blog polonês poderá perceber que lá havia várias considerações sobre a etimologia da palavra geloxia. Não coloco aqui essas observações pois a discussão com vários leitores que sabem muitas coisas referentes a etimologia mostrou que a questão é bastante complicada e incerta. Se algo ficar solidamente esclarecido, vou anexar as novas informações aqui mesmo. E por enquanto dou me por satisfeito com simples constatação: não sei e parece que os especialistas também não sabem.