
permite perceber que a composição de uma reflexão com translação (por um vetor não nulo) é uma isometria diferente daquelas que pertencem aos três grupos: rotações, reflexões, translações.
Portanto, justifica-se introdução de um novo nome de reflexão deslizante (“glide reflexion” em inglês).
No livro “Introduction to Geometry” H.S.M.Coxeter sugere visualizar as pegadas em um caminho reto na neve. Bem, ele era canandense… talvez uma sugestão de um caminho na praia levemente molhada fosse mais natural neste país.
Se reflexão é substituida por uma rotação, a situação é diferente. Vou mostrar que composição f de uma rotação não trivial com translação é uma rotação. Se o vetor for nulo, o fato é óbvio. Portanto consideramos o caso de ângulo diferente de zero e vetor diferente de nulo.
Denotamos D = f(C) e R = f(P).

O centro U daquela rotação encontra-se no cruzamento de bissetrizes de intervalos CD e PR (no esboço as bissetrizes têm nomes m e n).
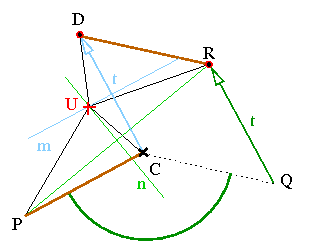
No começo mostro que a mesma rotação com centro em U leva C em D e P em R. Em seguida, provo que o ângulo dela é 2a, o ângulo da rotação usada em f.
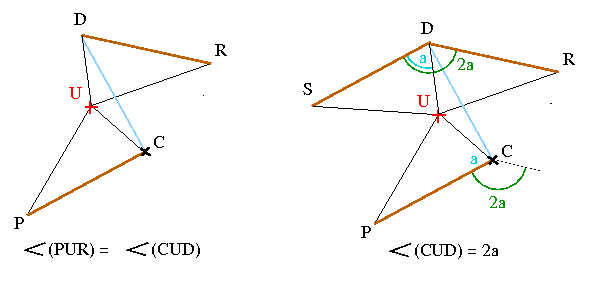
1. Já que U está na bissetriz de CD, tenho |CU|=|UD|. Também é verdade que U está na bissetriz de PR, então |PU|=|UR|. Finalmente, |CP|=|RD|=|t|, então os triângulos UCP e UDR são congruentes. Claramente segue daqui que os ângulos ang(PUR) e ang(CUD) são iguais.
2. Fixo em ponto D uma cópia do vetor CP perpendicular a CD. Tão como o triângulo UDR, o novo triângulo UDS é congruente a CUP. Mas os ângulos ang(PCQ) e ang(SDR) são iguais, então a=ang(UDS)=ang(UCP). Mas ang(PCD) é reto, portanto ang(UCD)=a', o ângulo complementar de a. Finalmente, ang(CUD)+2a' é soma de dois ângulos retos, quer dizer ang(CUD)=2a.
Caso você chegou a conclusão que demonstração elementar pode ser longa
demais (e para algumas pessoas isto é um sinônimo de “difícil”),
proponho aprender usar os números complexos. A noção é mais sofisticada,
mas o cálculo é curto. Composição de rotação por ângulo 2a
e translação por vetor t é descrita
como função w=ei2az+t. A afirmação
w=f(z) é uma rotação ao redor do ponto u
equivale a dizer:
u é o único ponto fixo, u=f(u), da função f.
De fato, equação z=ei2az+t tem a única (e imediata) solução u=t/(1-ei2a). Posso escrevé-la como
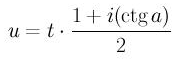
Notação introduzida na Algebra Linear também ajuda a compreender o sentido geométrico desta fórmula, pois reescrevendo-a em forma matricial:
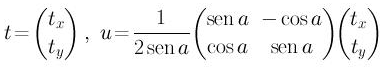
percebe-se que u surge do vetor t girado pelo ângulo a e atuando no obtido vetor com escalar [2sen(a)] -1.
