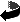![$ gen[ \begin{pmatrix}0&1\\ 1&0\end{pmatrix}\ \ ,\ \ \begin{pmatrix}1&0\\ 0&-1\end{pmatrix} ]\quad\subset\quad GL(2,\mathbb{Z})$](img6.gif)
Prove that all the groups below belong to the same isomorphism class.
![$ gen[ \begin{pmatrix}0&1\\ 1&0\end{pmatrix}\ \ ,\ \ \begin{pmatrix}1&0\\ 0&-1\end{pmatrix} ]\quad\subset\quad GL(2,\mathbb{Z})$](img6.gif)
Notation ![]() means group generated by the set U.
Having the inclusion
means group generated by the set U.
Having the inclusion
![]() in a group (or semi-group) X
it should be clear what is the operation on the set.
in a group (or semi-group) X
it should be clear what is the operation on the set.
![]() is the set of all possible functions
is the set of all possible functions
![]() .
.
![]() is the field of rational functions of the
variable x over field
is the field of rational functions of the
variable x over field
![]() .
.
![]() is the group of all invertible matrices
is the group of all invertible matrices ![]() with elements in field (ring)
with elements in field (ring)
![]() .
.
![]() denotes the presentation of the group:
denotes the presentation of the group:
![]() is a set of (abstract) generators, elements of
is a set of (abstract) generators, elements of ![]() together with their conjugates generate a subgroup that
is annihilated (kernel of
a homomorphism).
together with their conjugates generate a subgroup that
is annihilated (kernel of
a homomorphism).