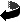![$ gen[ \begin{pmatrix}0&1\\ 1&0\end{pmatrix}\ \ ,\ \ \begin{pmatrix}1&0\\ 0&-1\end{pmatrix} ]\quad\subset\quad GL(2,\mathbb{Z})$](img6.gif)
Prove que todos os grupos descritos abaixo pertencem à mesma classe de isomorfismo.
![$ gen[ \begin{pmatrix}0&1\\ 1&0\end{pmatrix}\ \ ,\ \ \begin{pmatrix}1&0\\ 0&-1\end{pmatrix} ]\quad\subset\quad GL(2,\mathbb{Z})$](img6.gif)
Notação ![]() significa grupo gerado por elementos
do conjunto
significa grupo gerado por elementos
do conjunto ![]() . Tendo inclusão
. Tendo inclusão
![]() em um grupo
(ou semigrupo)
em um grupo
(ou semigrupo) ![]() fica claro de qual operação se trata.
fica claro de qual operação se trata.
![]() é o conjunto de todas as funções
é o conjunto de todas as funções
![]() .
.
![]() é o corpo de funções racionais da variável
é o corpo de funções racionais da variável ![]() sobre
corpo
sobre
corpo
![]() .
.
![]() é o grupo de todas as matrizes inversíveis
é o grupo de todas as matrizes inversíveis ![]() com
elementos em corpo (anel)
com
elementos em corpo (anel)
![]() .
.
![]() denota a apresentação (presentation) de um grupo:
denota a apresentação (presentation) de um grupo:
![]() é um conjunto de (abstratos) geradores, os elementos de
é um conjunto de (abstratos) geradores, os elementos de ![]() junto com os seus conjugados geram um subgrupo que
é aniquilado (núcleo de um homomorfismo).
junto com os seus conjugados geram um subgrupo que
é aniquilado (núcleo de um homomorfismo).