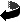![$ gen[ \begin{pmatrix}0&1\\ 1&0\end{pmatrix}\ \ ,\ \ \begin{pmatrix}1&0\\ 0&-1\end{pmatrix} ]\quad\subset\quad GL(2,\mathbb{Z})$](img6.gif)
Pokaż, że te wszystkie grupy należą do tej samej klasy izomorfizmu.
![$ gen[ \begin{pmatrix}0&1\\ 1&0\end{pmatrix}\ \ ,\ \ \begin{pmatrix}1&0\\ 0&-1\end{pmatrix} ]\quad\subset\quad GL(2,\mathbb{Z})$](img6.gif)
Zapis ![]() znaczy grupa wygenerowana przez zbiór U.
Powinno być jasne jaka jest operacja grupowa gdy jest inkluzja
znaczy grupa wygenerowana przez zbiór U.
Powinno być jasne jaka jest operacja grupowa gdy jest inkluzja
![]() w grupie X.
w grupie X.
![]() to zbiór wszystkich funkcji
to zbiór wszystkich funkcji
![]() .
.
![]() to ciało funkcji wymiernych zmiennej
x nad ciałem
to ciało funkcji wymiernych zmiennej
x nad ciałem
![]() .
.
![]() to grupa wszystkich odwracalnych macierzy
to grupa wszystkich odwracalnych macierzy ![]() z elementami w ciele (lub pierścieniu)
z elementami w ciele (lub pierścieniu)
![]() .
.
![]() oznacza prezentację grupy:
oznacza prezentację grupy:
![]() to zbiór (abstrakcyjnych) generatorów, elementy z
to zbiór (abstrakcyjnych) generatorów, elementy z ![]() razem ze sprzężonymi z nimi generują podgupę, która jest
wyzerowana (jądro homomorfizmu).
razem ze sprzężonymi z nimi generują podgupę, która jest
wyzerowana (jądro homomorfizmu).