Inicialmente haverá poucas coisas aqui, mas isso é natural. Como disse o filósofo chinês Lu La, “por mais longa que seja a caminhada ao céu, ela tem que começar com um simples pulo para Washington”.
Qual desses dois números é mais fácil? (para aproximar por números racionais, para construir geometricamente, para manusear em uma fórmula, para pendurar na parede, para sei lá o que.)
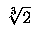
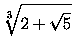
Se você não quer se comprometer e prefere ficar em cima do muro, aqui está uma reformulação da pergunta: qual desses dois números pode ser a tal de “proporção áurea”?
Quem diria que neste inocente exercício de Martin Gardner:

a resposta é exatamente mesma que no caso da pergunta:
mas as duas perguntas são completamente desconexas?
Por sinal, o Mestre M.Gardner, propondo o exercício na edição de setembro 2000 da revista The College Mathematics Journal, forneceu para o editor dela, Prof. Underwood Dudley, uma resposta mais redonda (50 peças) mas menos correta …
No dia 16 de junho 2002 foi atingida a marca de 800 livros-textos universitários de filosofia que contém uma afirmação equivalente à frase seguinte: “pitu-pitu, pitu-pitu, como na matemática que com certeza absoluta confirma que 2+2=4”. Se acreditar nas profecias de Nostradamus, na hora que a quantidade de tais textos ultrapassar o número 210, haverá o absoluto e inevitável fim do mundo pela explosão de saco cheio de matemáticos de vários países.
Você acha que isto é parecido com os desenhos da série Proofs without words (“Demonstrações sem palavras”)?
| PROBLEMA | SOLUÇÃO |
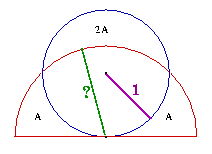 |
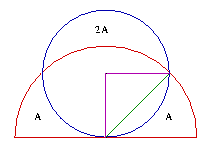 |
Talvez pareça mas não é. O desenho à direita não é uma demonstração. Vendo o esboço fica evidente qual é a solução mas não há indicação qualquer como chegar a este resultado - isto é, como conferir a veracidade da afirmação transmitida pelo desenho.
Suspeito que algum tipo de cálculo (e não somente um argumento desenhado) seja aqui inevitável. Estou ciente disso que constatações desse gênero são bastante arriscadas, pois não tomam em conta a fantasia e criatividade de pessoas que gostam da matemática, tanto profissionais quanto leigos. Mesmo assim, exponho esta sugestão, pois sei como produzi o esboço à esquerda que propõe o problema. Esta versão do desenho que você está vendo foi feita quando eu já sabia da resposta. A versão inicial que poderia ter mais ou menos esta forma:
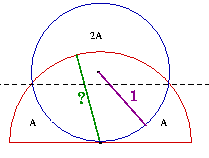 |
e isso não levaria a solução alguma desse gênero: |
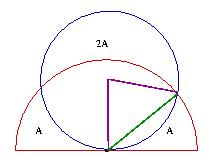 |
Com respeito ao cálculo, a geometria sintética (ou “quantitativa”, como dizemos no nosso curso) leva à resposta em 30 segundos. O uso de geometria analítica levaria 3 minutos, portanto aposto que 80% de alunos de segundo grau e 90% de estudantes universitários começariam introduzindo as coordenadas cartesianas.