Teorema de Tales em cinco atos

Didascália

Escola de primeiro grau, a primeira aula é de matemática. Entra Klara, uma professora simpática e alegre, mas todas as crianças ficam tensas. Vai ter o teorema de Tales.

Se tudo correr bem, Klara permanecerá na memória dos alunos bem lembrada. Se correr mal, haverá tédio e reclamações. A questão é se entre os alunos está o João Espico. É o apelido, abreviação do Espírito Contestador. Klara gira cabeça e enxerga-o. Sente os calafrios pois não sabe que justamente graças ao João Espico ela vai se tornar uma boa profissional.

O primeiro ato revelará que a linguagem da matemática, seca e rígida, não foi inventada para torturar os humanistas mas é um sistema de defesas contra os Espicos de várias espécies que com leves toques derrubam os artigos da fé e os conteúdos didáticos da Klara.

Pois é, a sala está cheíssima, em primeiras filas estão sentadas Meninas Obedientes que confirmam tudo e concordam com tudo. Nas últimas filas ficam os Meninos Cínicos que estão mandando um para outro SMS.

Ato I. Primeiro grau

Klara. Lembram-se que no ano passado andsol explicava o sentido do teorema de Tales?

Crianças. Lembramos. De nada. O que é o andsol?

Klara. Isso mesmo, a gente dizia que quando temos no plano figuras, pouco importa se vemos o plano de perto ou de longe, para quem está dentro nada muda. Se um traço foi oito vezes maior do outro, tudo fica do mesmo jeito mesmo se nos afastamos por um quilômetro. Ou de outro jeito, em vez de falar de que a gente se afasta pensamos assim: alguém fez uma cópia do plano e aumentou tudo cem vezes. Os traços são mais longos mas eles estão – como costumamos de dizer – na mesma proporção, oito a um. E Tales teve a idéia que será suficiente contar isso só com os triângulos e a regra ficará clara para todas as figuras no plano. Então tentaremos desenhar isso no quadro negro. Pensei que vocês poderiam me ajudar. Imaginem que isso é uma receita culinária de um bolo na tv. Eu vou falando o que tem que ser feito e alguém vai desenhar isso no quadro-negro. Sim, Espico, qual problema?

Espico. Eu posso desenhar pois já tenho as mãos sujas.

Klara (com um momento de pânico controlado) Mas claro, Espico, vem cá e pegue o giz azul, no começo vamos traçar as semi-retas azuis. Pronto?

Espico (pega o giz olhando ironicamente). Muito pronto.

Klara. Queremos ter um ângulo então desenhamos duas semi-retas.

Espico.

Klara (de fato, eu não disse que elas têm começo comum). Desenhamos duas semi-retas que partem do mesmo lugar.

Espico.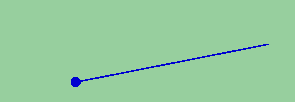

Klara (precisa de alguns segundos para entender que Espico escondeu uma semi-reta por baixo da outra.) Bem, uma semi-reta não cobre a outra porque elas não são idênticas.

Espico.

Klara. Vou dizer isso de outro jeito: desenhamos duas semi-retas que não são paralelas e partem do mesmo ponto.

Espico.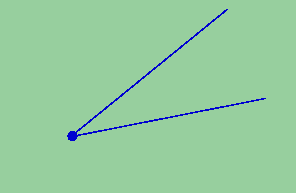

Klara. Excelente! Agora, Espico, vamos desenhar duas retas. Vão ser duas retas paralelas. Melhor usar uma outra cor para elas, que tal marrom? Desenhamo duas retas, paralelas, (esta vez não vou esquecer!) que não ficam uma escondendo a outra e ambas as retas encontram ambas as semi-retas.

Espico.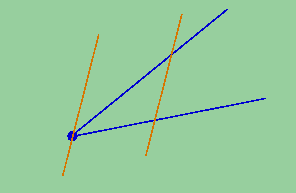

Klara (não, isso não pode ser um acaso. O que é que ele tem no caráter que consegue torcer tudo que se falar para ele?) Talvez eu diga assim: estas retas não devem passar pelo ponto de partida das semi-retas.

Espico.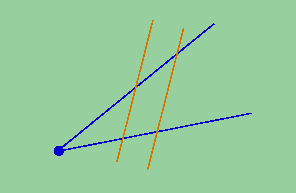

Klara (quase chorando de alívio e alegria) Belíssimo. Agora em uma das semi-retas marcamos dois intervalos; ambos eles começam no início da semi-reta e terminam lá onde encontram as retas.

Espico.

Klara. Posso dizer que um intervalo é mais curto e outro mais longo? Isto é claro?

Crianças. Sim! Não! Tanto faz! Sei lá. Flamengo ganhou três a um.

Klara. Vamos dividir os comprimentos mas não vamos escrever nada, só na memória. Digamos que dividimos o número maior pelo número menor.

Zé Zagueiro. E qual número é maior, do pedaço mais curto ou do mais longo?

Espico (baixinho). Cai fora, Zé. Eu derrubo tudo cientificamente e você me entra com besteirol.

Klara. Parem, meninos. Zé, o João Espico te explicou tudo? Ótimo. Lembrem que tal número se chama o quociente ou escala ou coeficiente de proporção ou ...

Alguém do fundo. Nossa, porque tantos nomes para um número?

Klara. Você tem razão, um é bastante. Então vamos falar do quociente ou da razão numérica. Agora, marcamos nas retas dois intevalos contidos entre as semi-retas.

Espico.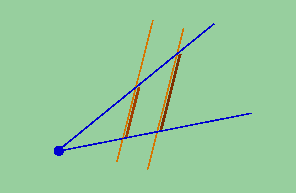

Klara. Ficou claro que um destes intervalos está mais comprido?

Crianças. Não! Sim! No domingo Flamengo vai perder!

Klara. Vale a pena desenhar separadamente só os dois pares de intervalos que recortamos nas semi-retas e nas retas.

Espico.

Klara. Para os novos intervalos também fazemos o quociente, dividimos o comprimento maior por menor. E agora – estou curiosa quem de vocês adivinha o que vai acontecer?

Crianças. Amanhã não haverá aulas! Vai vir um novo professor! A mãe do Espico terá que vir para conversar com o diretor!

Klara. Não, queridos. Os dois quocientes que obtemos...

Menina Obediente. ...são dois números iguais. Professora, dois números diferentes podem ser iguais?

Klara. Os números são mesmos, as notações podem ser diferentes. Duas cópias do mesmo número as vezes têm aparência diferente. Por exemplo 7/2 e 21/6, você concorda?

Menina Obediente. Professora, eu sempre concordo.

Klara. Então vai concordar que para o intervalo e para o seu comprimento vamos dar o mesmo nome. Isto é uma convenção não muito certa mas prática e todo mundo faz assim.

Espico (assobiando). Posso já sentar?

Klara. Você não quer dar ainda nomes àqueles intervalos e marcar isso no desenho?

Espico. Posso, eu não ligo. De qualquer modo tenho sujado a blusa. Bem, tenho nomes bem divertidos para eles: a,b,c,d. Bonito?

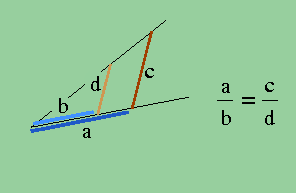
Klara. Obrigado, João Espico, fizemos um bom trabalho. Vou contar tudo mais uma vez – mesmo se alguém passasse esta descrição por telefone para Austrália...

Alguém do fundo. Meu tio vive na Austrália e tem um carro de dez metros.

Klara ...mesmo assim o desenho feito lá seria basicamente o mesmo que aqui. Então. Começamos com algo que chamamos de hipóteses. Elas estão aqui: pegamos duas semi-retas não paralelas que começam em um ponto e pegamos duas retas distintas mas paralelas que não contêm aquele ponto e que encontram cada uma das semi-retas. Em uma das semi-retas pegamos dois intervalos, do ponto inicial até os pontos de encontro com as retas. Nas retas pegamos dos intervalos contidos entre semi-retas. Para cada par de intervalos formamos o quociente dividindo o comprimento maior pelo comprimento menor. E agora vem a tese, quer dizer, isso que afirmamos sobre a nossa figura: os dois quocientes estão iguais.

xxxxxxxxxxxxxxxxxxxxxxxxxxxxx

Um momento de limpeza após o primeiro ato. Alguns livros contêm desenho com um monte de retas paralelas. Qual o sentido de chamar ao palco muitos figurantes se precisa-se só de dois atores? Para a peça custar mais caro?

Há casos que alguém assim desenha o teorema:

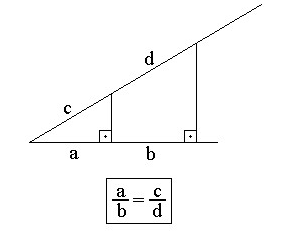
Isto é uma idéia MUITO ruim. Desse modo cria-se em crianças um preconceito, uma convicção que o teorema vale só quando as retas encontram uma das semi-retas formando um ângulo especial: o ângulo reto.

Ato II. Segundo grau

Aparece a notação vetorial: a gente multiplica o vetor u pelo escalar (um número, digamos que um número positivo) k. E aparece uma fórmula simples que lembra “a lei de distributividade de adição com respeito de multiplicação” ou pelo contrário (nunca me lembro, tanto faz, melhor esquecer) dizendo que para cada número k e para todos os vetores u, w, temos k(u+w) = ku+kw. Surpresa: isto é o teorema de Tales. De fato, muito mais, pois permitimos (não proibimos, portanto permitimos) que u e w sejam paralelos. E já que aparece lá o símbolo “=”, temos também o teorema inverso ao teorema de Tales!

Ato III. Universidade

Descobrimos neste nível que todas as “demonstrações” do teorema de Tales não passavam de um engodo mesmo se os educadores acreditavam que estiveram provando alguma coisa. Se os intervalos mais curtos são conmesuráveis (a razão dos comprimentos pode ser expressa por meio de proporção dos dois números naturais), pode-se rechear o esboço e conferir que na vertical e na horizontal há a mesma quantia de triangulinhos. Mas se a razão é irracional, nada feito; precisa-se de axioma sobre existência do limite supremo no conjunto delimitado, quer dizer, o axioma sobre a continuidade da reta. Neste caso fica mais simples assumir a veracidade da afirmação de Tales, obtendo o axioma de Tales equivalente ao axioma sobre a existência do limite supremo. Mas as crianças continuam sendo enganadas...

Ato IV. Pós-graduação, nível de mestrado

(Assumindo que a universidade vale este nome e ensina estas coisas no curso de teoria de grupos ou de álgebra.)

Escrevendo desse jeito, o teorema de Tales: f(x+y) = f(x)+f(y) (no caso elementar a função f é a atuação de um escalar) revela-se como protótipo da noção de homomorfismo. É a fonte de todos os homo, iso, endo e epi morfismos. E na escola o negócio teve a aparência tão inocente...

Ato V. Pós-graduação, nível de doutorado

Temos duas categorias com morfismos, digamos: álgebra com homomorfismos e topologia com funções contínuas. E consideramos um funtor entre elas tal que... Incrível, sempre a gente está mexendo com o mesmo teorema de Tales? Isso nunca terá o fim?

Peça acabou. Na porta dos Ceús São Pedro confirma que a transferência da Terra para a vida eterna está descrita por uma variante do axioma de Tales...