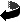...antes de mais nada os diagramas servem para auxiliar o olho e a mente graças a natureza intuitiva do seu testemunho...foi plenamente alcançado, já que 120 anos mais tarde todos os livros elementares de matemática usam este caminho para introduzir alunos em Teoria de Conjuntos.
Em geral usa-se dois diagramas na escola:
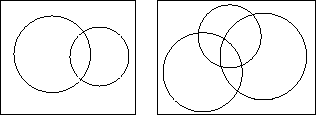
Muito menos conhecido é o diagrama que representa as possíveis relações entre 4 conjuntos, da autoria do próprio Venn, que constatou que esta vez 4 círculos não dariam a conta do recado e fez a escolha bastante natural da elipse como a figura que iria substituir o círculo.
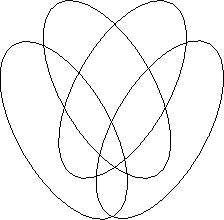
Em seguida fez a observação que nem elipses servem para 5 conjuntos e propôs para este caso o uso de figuras em forma de ferradura.
Acontece que esta afirmação é visivelmente falsa, visivelmente - se você olha para esta visualisação que não deixa de ser um diagrama de Venn:
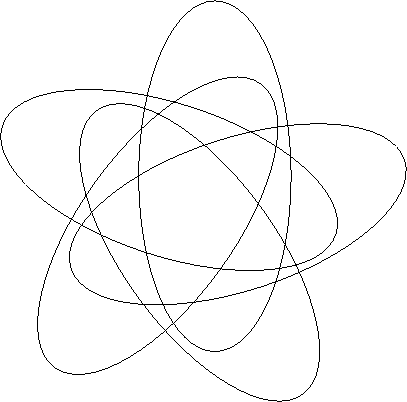
A não-existência desta configuração era reafirmada várias vezes em textos matemáticos durante os seguidos 95 anos até que Branko Grünbaum a inventou e divulgou. (Veja o artigo Venn Said It Couldn't Be Done de Peter Hamburger e Raymond E.Pippert em Mathematics Magazine, vol.73, nº2, April 2000, p.105-110. A nossa Biblioteca Universitária não assina esta revista mas você pode encontrá-la na sala do PET.)
Exercício 1. Descreva em todos os 4 diagramas as áreas recortadas usando uma numeração de conjuntos envolvidos. O objetivo é de associar o caso de diagrama com n objetos com um conjunto de números que usam (ou não usam!) os algarismos 1,...,n. Tendo esta descrição, ressalta aos olhos quantas áreas podemos ter em caso geral de n qualquer.
Exercício 2. Para cada dos diagramas colore as áreas usando as cores diferentes para encontro de duas ou três ... etc figuras (por exemplo usando as cores cada vez mais escuras). Faça uma tabela colocando em linhas as consecutivas quantias de áreas de cada das cores, as consecutivas linhas correspondendo ao número crescente de figuras envolvidas.
A idéia de representar uma configuração de três conjuntos por meio de três círculos parece hoje óbvia mas há 120 anos era inovadora. Mas o que era tão inovador nela? Afinal, a configuração era muito conhecida - um dos motivos disso era o fato que servia como um símbolo da união da família italiana Borromeo da região de Piemonte, famosa e influencial no período da Renascença:

A sua simbólica é bastante clara: removendo um dos círculos os demais não são mais unidos; além disso a impossibilidade de construir o modelo da configuração usando os círculos não distorcidos acrescenta algo místico á idéia.
(Sobre outras manifestações dessa configuração, consideravelmente anteriores ao século XIX, veja no borromean.html de onde a ilustração foi emprestada. Seguramente vale a pena dar uma lida do côdigo html deste arquivo, há algumas preciosidades no texto comentado (escondido) pelo autor.
Para que falar sobre tudo isso?
Bem, acredito que a estória revela (para quem está interessado em revelações) algumas idéias importante sobre a matemática. Por exemplo (um truísmo para psicólogos que mexem com a psicologia cognitiva) que por mais original que uma idéia pode ser, no fundo ela apenas reorganiza o material já existente; que um erro bem encravado durante longos anos é possível na vida dos matemáticos; e se acreditar no ditado que “a matemática é o que os matemáticos andam fazendo” então um erro pode fazer parte da matemática, tida por leigos como refúgio sacrossanto, livre de erros e imperfeições; que um fato ou objeto pode existir durante longo período antes de revelar o seu lado útil em uma maneira inesperada.