Sobre coisas estranhas

Reconheço que os cientistas não têm a mesma opinião sobre “estranho e natural” que um típico apreciador do programa Fantástico. Fico admirado quando vejo alguém que separa gema da clara usando apenas o poder do pensamento – mas surpreende-me nisso o fato que alguém gasta 3 horas e 4 kg de peso por causa do esforço mental para fazer o mesmo que eu faço com uma faca e a própria casca do ovo em 10 segundos. Por outro lado várias pessoas não verão graça alguma em multiplicação de dois números por meios geométricos - e para mim isso é algo fascinante. Estou me referindo ao resultado tão trivializado hoje em dia que pode servir de um simples exercício no começo do curso – veja o exercício 6 da página 9 e as observações que o precedem. 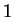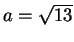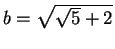Para esclarecer o motivo do meu fascínio: imagine que partindo do intervalo que tem comprimento você chegou produzir outros intervalos com comprimentos e – o teorema de Pitágoras e a construção do pentágono regular podiam levar a este resultado. Suponha agora que por algum motivo você decidiu visualisar (interpretar geometricamente) o número . 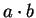O uso rotineiro do teorema de Tales resolve isso em poucos instantes. Esse teorema é conhecido desde 2600 anos - então pode-se concluir que os cidadões da antiga Grécia ou Roma – ou a turma do Pedro Álvares Cabral – podia fazê-lo a vontade? Nada disso. Ao longo de 2000 anos entendia-se que a única interpretação geométrica do produto de dois comprimentos é uma área do retangulo com as adequadas arestas. Foi uma enorme surpresa quando por volta de 1640 Descartes sugeriu a receita para essa visualição. Uma parte da surpresa (chame-a de “social”) reside no fato que aparentemente ninguém se deu conta disso durante 2000 anos – mesmo que o teorema de Tales fazia parte indispensável da instrução; mas a maior motivo da surpresa (chame-o de “técnico”, se quiser) reside no seguinte: parto das noções que se referem a reta, ai também termino. Mas o meu caminho obrigatoriamente me leva por uma construção planar. Problemas da dimensão um resolve-se usando meios da dimensão dois.