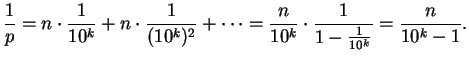Comprimento de período de 1/p para p primo
A questão é como justificar o seguinte fato (válido em qualquer sistema
posicional, mas aqui mostrado para o sistema decimal):
para 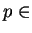
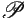 o comprimento
o comprimento 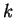 do período
do período
da representação de
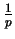 é um divisor de
é um divisor de 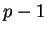
sem usar as noções da teoria de grupos. Pelo menos na superfície, pois
o cerne do argumento é o pequeno teorema de Fermat :
se 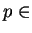
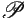 e
e 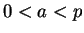 então
então
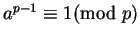 .
.
Vamos pelos passos pequenos e triviais. Tem que ter um periodo
e não pode ser mais longo que p-1, pois no processo de divisão podem
aparecer restos entre 1 e p-1, e na primeira reaparição
de um deles o ciclo recomeça.
Digamos que obtivemos o periodo
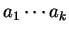 . Trate este bloco de algarismos como número
n em notação decimal.
Isso significa que
. Trate este bloco de algarismos como número
n em notação decimal.
Isso significa que
Portanto,
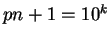 , ou
, ou
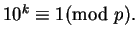
Agora, pode-se reformular a frase
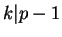 dizendo
dizendo
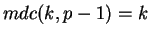 .
Contradizer esta afirmação significaria dizer
.
Contradizer esta afirmação significaria dizer
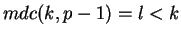 .
Mas a identidade de Bézout garante a existência
de
.
Mas a identidade de Bézout garante a existência
de 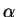 e
e 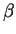 inteiros tais que
inteiros tais que
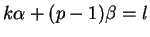 . Nesse caso ter-se-ia
. Nesse caso ter-se-ia
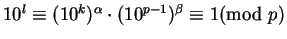 .
Mas isto quer dizer que na
.
Mas isto quer dizer que na 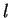 -ésima divisão por
-ésima divisão por 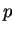 reaparece o resto
reaparece o resto 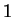 ,
contradizendo a hipótese que
,
contradizendo a hipótese que 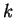 é o periodo.
é o periodo.
Freqüentemente chama atenção o fato que surge
uma permutação cíclica de algarismos de
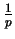 quando considera-se
quando considera-se
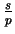 com
com 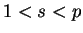 .
.
Multiplique a expressão obtida para
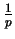 por
por 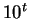 com algum
com algum 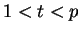 . Jogue fora
. Jogue fora
![$ [10^{t}\cdot\frac{1}{p}]$](img27.gif) (a parte inteira) - e você fica com
(a parte inteira) - e você fica com
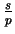 onde
onde
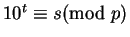 .
.
Fpolis, 1998
Acrescentei
aqui
tabela que na linha n mostra quais
são os primos que dividem 10n-1 e não apareceram
como divisores do número desta forma com expoente menor; portanto para tal
primo p o número n é o comprimento do seu período.
Fpolis, 2010


![]() . Trate este bloco de algarismos como número
n em notação decimal.
Isso significa que
. Trate este bloco de algarismos como número
n em notação decimal.
Isso significa que