The Fermat Point of a Triangle
If you prefer concise stories, take a look at p.83 of Geometry Revisited by H.S.M.Coxeter and S.L.Greitzer.
 |
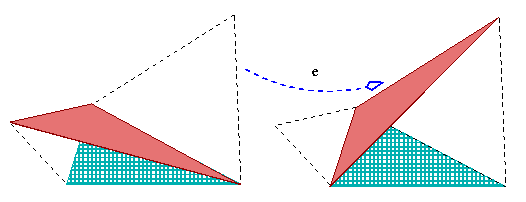
Do you recall Pete Seeger's song “If I had a triangle”? Well, suppose you have one and you decide to glue some nice forms to its sides. |
| Using squares you get a pleasing design but this time you would rather do without Pythagorean theorem and the cosine theorem. You want to hit new lands. Why not to try equilateral triangles? |
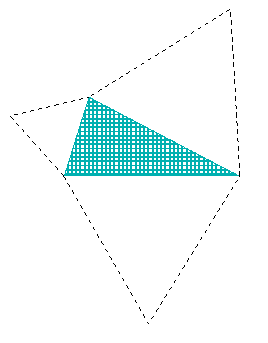
|
|
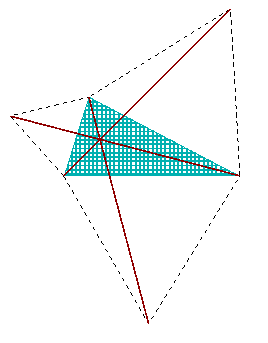
They seem to open like petals of a flower. And each of them forms
a quadrilateral with the initial triangle. So there comes an idea:
how would it look if one drew their diagonals?
(Did you expect me to talk about Napoleon's theorem? No, I would rather deal with diagonals this time. The initial sketch is in fact the same but the story is different.) |
Are the lines too thick or do the diagonals really meet in one point? Perhaps it takes a bit of time to find out. But it may be amusing to try.
However, a suspicion arises. Does the supposed crossing point always lie inside of the triange? Some experiments with pencil and compass show that it might go for a walk. It is clear enough that the sketch changes completely when one of the angles reaches 120°.
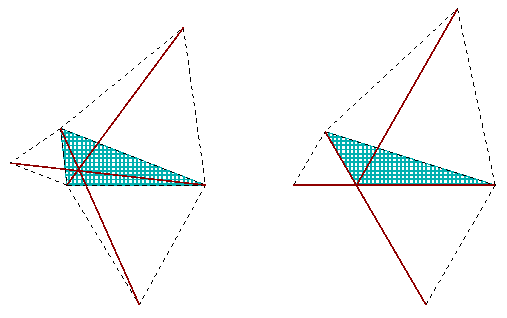
One thing at a time. While the meeting point is in question, we had better stay inside of the triangle. Therefore do agree, please, that we bar from our examinations the triangles having an angle of 120° or even more.
| The angles of 60° and 90° will enter the stage. (You call them Pi/3 and Pi/2? So do I.) It might save time to have shorter names for them. Let me mark them with letters e and r (just for plain “equilateral” and “right”). And skip one of the petals for a time. Doesn't it become really scientific? | 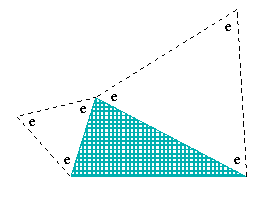 |
So, the angle is e:
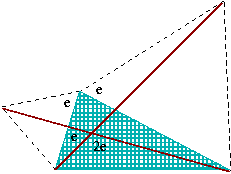 - the one you have in petals.
- the one you have in petals.
It bells a familiar ring (or even two of them):
Yes, it comes from the reverse of the theorem on the central angle (based on a chord). The conclusion is that both circles that circunscribe two equilateral triangles catch also F, the meeting point of two diagonals.
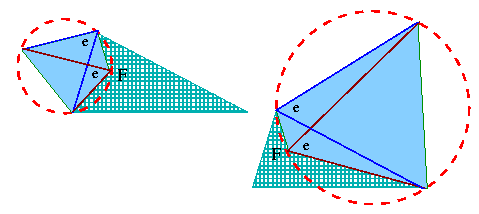
Is the time right to call the third diagonal on the stage? Just a moment, there is something more that you already know:
| There is another quadrilateral with vertex F that can pose all its vertices on a circle! (The technical term for such polygonal figure is “cyclic”.) Just recall this neat condition: the opposing angles of the quadrilateral must add up to 2r. A new theorem? Not really, it is another follow-up of the theorem on the central angle. Therefere check that 2a + a = 2r to be certain that drawing another circle is possible: |
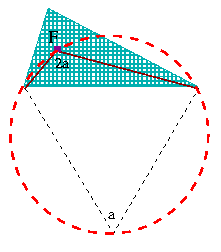
|
And now, there comes the angle between the first and the third diagonals. One more swing, please! The clockwise one, this time:
| The new meeting point lies also on the circle around the third equilateral triangle. The circle cannot meet a line (the first diagonal) more than twice. And two points of intersection are already there! One is F and the other one is the triangle vertex lying on the right-side edge. | 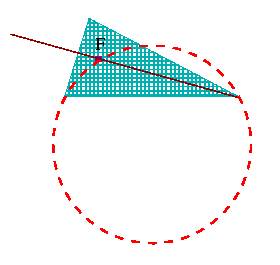 |
| Good. The new meeting point is not on the edge (we agreed that the angles do not reach 120°, didn't we?), so it must coincide with F. We have got it: all three diagonals meet at F, each pair making the angle 2a. | 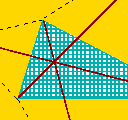 |
Such a distinguished point deserves a distinguished name - in fact, F is called the Fermat point of the initial triangle. |
Although it catches one's attention as a meeting poing of three diagonals, just one of the diagonals and one circunscribing circle are necessary to locate the Fermat point of a triangle:
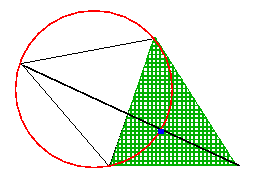
And what is the reason for the choice of the name? It is a question
of Pierre Fermat, asked some 370 years ago:
for which point in an acute-angled triangle the sum
of distances to the vertices will be as small as possible?
Well, this is how most sources have it. Still, Internet materials diverge in details. The information in Eric Weisstein's encyclopedia
This problem [...] was proposed by Fermat to Torricelli. Torricelli's solution was published by his pupil Viviani in 1659
may be correct but is it what actually Fermat wrote? I find that much more instructive is the passage in Harold W. Kuhn's posting. He wrote that Fermat's challenge was:
“Given three points in the plane, find a fourth point such that the sum of its distances to the three given points is a minimum!”
A very short story on a result of Vicenzo Viviane will appear here later. What makes me cite all those names and connections? Fine, Fermat challenges Torricelli (short-time assistant to Galileo), his pupil is Viviani - so what? Well, you see that they knew each other and you wonder: was it so small world or did they do their best to stay in touch long before the advent of the Internet?
Calculational solution is rarely presented. The one I know of is from 1994, it is an article by Mowaffaq Hajja “An Advanced Calculus Approach to Finding the Fermat Point”, in the February issue of Mathematics Magazine. Usually you approach the problem geometrically.
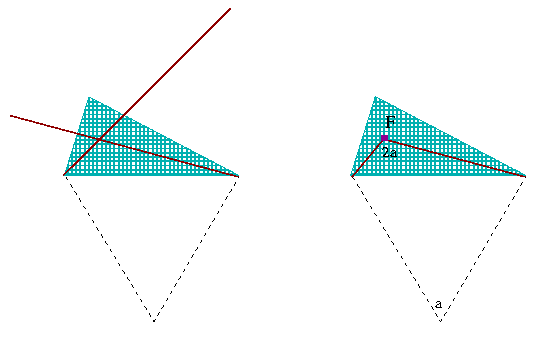
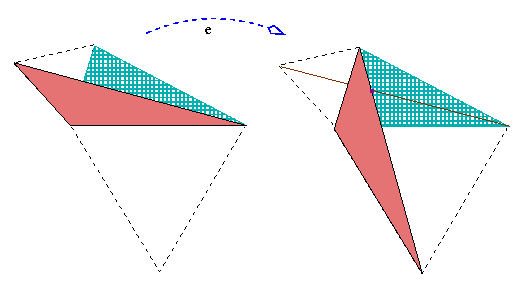
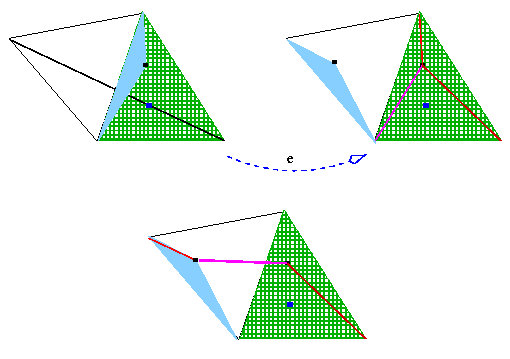
A smart idea applied in the construction below might convince you that “aesthetic appeal” or “nice shape” need not oppose “simple and efficient reasoning”.
Choosing any point inside of the triangle, the sum of three distances is the same as the length of the broken line that shares its extremities with the diagonal.
Well, if the Fermat point is choosen, the broken line straightens up!
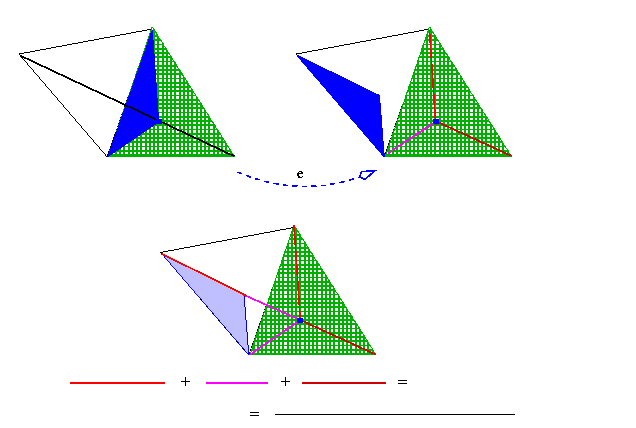
So, this is the choice that gives the smallest possible sum.
In addition, you see that any of three diagonals would serve in the construction - so all three of them have the same length!
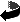 mathematics
mathematics
