Punkt Fermata w trójkącie
Jeśli wolisz zwięzłe opowieści, zerknij na str.83 Geometry Revisited; autorzy to H.S.M.Coxeter i S.L.Greitzer.
 |
Pamiętasz pieśń Pete'a Seegera „Gdybym miał trójkąt”? Powiedzmy więc, że masz trójkąt i postanawiasz dolepić do jego boków jakieś miłe formy. |
| Używając kwadratów dostaje się przyjemny wzorek ale tym razem wolisz zostawić na uboczu twierdzenie Pitagorasa i twierdzenie kosinusów. Zamierzasz odwiedzić nowe lądy. To może by spróbować trójkątów równobocznych? |
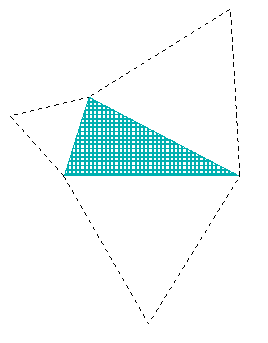
|
|
Robi wrażenie, że otwierają się jak płatki kwiatu. I każdy z nich
tworzy czworobok razem z początkowym trójkątem. Nasuwa to pomysł:
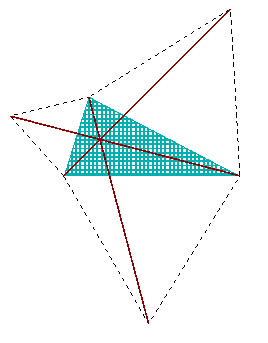
jakby to wyglądało gdyby im dorysować przekątne?
(Zanosiło się na to, że będę mówił o twierdzeniu Napoleona? Nie, wolałbym tym razem zająć się przekątnymi. Przyznaję, że początkowy szkic jest taki sam, ale historyjka jest odmienna.) |
Czy to kreski są zbyt grube czy też przekątne w istocie spotykają się w jednym punkcie? Sprawdzenie tego może zająć nieco czasu. Ale próba może być dobrą rozrywką.
Jednak pojawia się pewne podejrzenie. Czy zawsze ten rzekomy punkt krzyżowania się leży wewnątrz trójkąta? Parę doświadczeń z użyciem ołówka i cyrkla pokazują, że może udać się on na przechadzkę. Jest jasne, że rysunek zmienia się całkiem gdy jeden z kątów dochodzi do 120°.
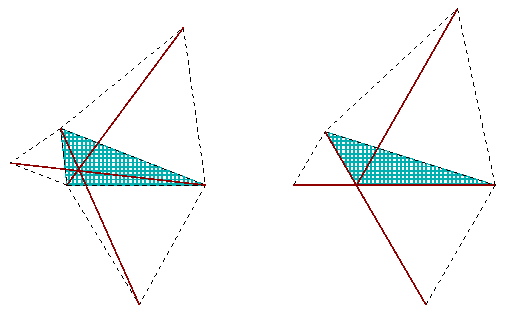
Nie chcesz mieć paru problemów naraz? Więc zastanawiając się czy jest jeden punkt spotkania, chcemy zostać wewnątrz trójkąta. Zgódź się więc, że wykluczymy z naszych rozważań trójkąty mające kąt mierzący 120° lub więcej.
| Pojawiają się na scenie kąty 60° i 90°. (Nazywasz je Pi/3 i Pi/2? Ja też.) Zaoszczędziłoby czasu gdyby miały one krótsze nazwy. Czy mogę oznaczyć je literami e i r? I na chwilkę odrzucę jeden z płatków. Czyż to nie zaczyna wyglądać bardzo naukowo? | 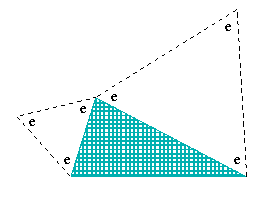 |
A więc kąt to e:
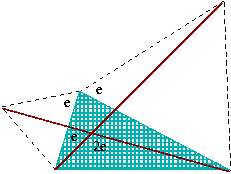 - tak jak w płatkach.
- tak jak w płatkach.
Przypomina to szkolny rysunek z okręgami:
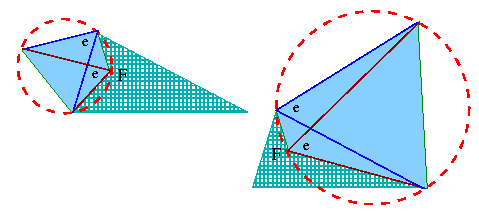
Tak, to bierze się z odwrócenia twierdzenie o kącie środkowym (opartym na cięciwie). Widać stąd, że oba okręgi wokół trójkątów równobocznych („opisane na nich”, w technicznym języku) chwytają też F, punkt gdzie przekątne spotkają się.
Czy byłby już czas by przywołać trzecią przekątną na scenę? Chwileczkę, jest tu jeszcze coś, co już wiesz:
| Jest tu i inny czworobok z wierzchołkiem F, który ma wszystkie swoje wierzchołki oparte na okręgu! (I znowu język techniczny przynosi tu swój termin, mówi się o takich wielobokach, że są „cykliczne”.) Przypomnij sobie to proste wymaganie: przeciwległe kąty czworokąta muszą dać w sumie 2r. Jeszcze jedno twierdzenie? Właściwie nie, to inna korzyść z twierdzenia o kącie środkowym. Więc dla potwierdzenia, że da się opisać tu nowy okrąg sprawdzamy, że 2a + a = 2r. |
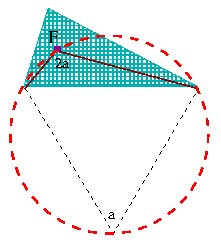
|
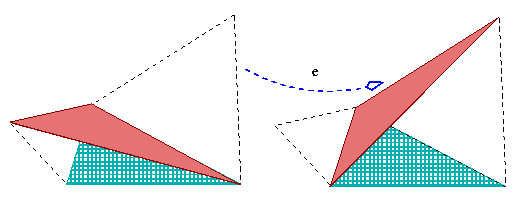
No i teraz pojawia się kąt między pierwszą i trzecią przekątną. Znowu zakręcimy trójkątem - ale tym razem w innym kierunku:
| Także i nowy punkt zetknięcia się leży na okręgu zatoczonym wokół trzeciego trójkąta równobocznego. Ale okrąg nie może spotkać się z odcinkiem więcej niż dwa razy. I są już dwa punkty spotkań: jeden z nich to F a drugi to wierzchołek trójkąta leżący po jego prawej stronie. | 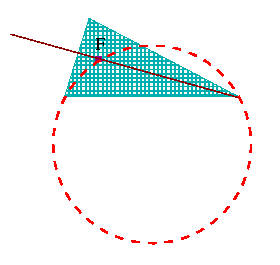 |
| Świetnie. Nowy punkt kontaktu nie jest na krawędzi (zgodziliśmy się, że kąty będą mniejsze niż 120°, nieprawda?), więc musi to być F. A więc w istocie masz pożądany wynik: trzy przekątne przecinają się w F, każda ich para tworzy kąt 2a. | 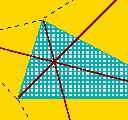 |
Tak wyjątkowy punkt zasługuje na wyjątkową nazwę. I rzeczywiście, F jest znany jako punkt Fermata wyjściowego trójkąta. |
Choć spotykanie się trzech przekątnych w jednym miejscu zwraca uwagę, można w trójkącie usytuować punkt Fermata używając jednej z przekątnych i jednego z okręgów:
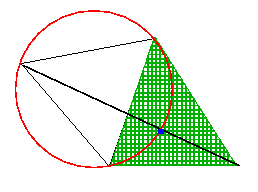
A skąd wziął się wybór jego nazwy? To z powodu pytania, które zadał
Pierre Fermat ponad 350 lat temu:
dla którego punktu wewnątrz ostrokątnego trójkąta
suma odległości do wierzchołków jest najmniejsza?
No, przynajmniej tak to jawi się w większości odnośników. Ale materiały internetowe rozbiegają się w szczegółach. Informacje z encyklopedii Erica Weissteina:
Problem ten [...] Fermat przedstawił Torricelliemu. Rozwiązanie Torricelliego zostało opublikowane przez jego ucznia Vivianiego w roku 1659
może jest poprawne ale co naprawdę napisał Fermat? Wydaje mi się dużo bardziej pouczającym ten urywek w liście Harolda W. Kuhna z listy dyskusyjnej. Pisze on, że wyzwanie Fermata tak brzmiało:
„Dla danych trzech punktów na płaszczyźnie, znaleźć czwarty punkt taki, że suma odległości jego do trzech danych punktów jest najmniejsza możliwa!”
Bardzo krótka historyjka o pewnym wyniku geometry Vicenzo Viviani pojawi się tu później. Lecz po co cytować te wszelkie nazwiska i powiązania? No, Fermat stawia wyzwanie Torricelliemu (który przez krótki czas pracował dla Galileo), ten miał ucznia Vivianiego - i co z tego? Otóż gdy widzisz, że oni znali się wzajemnie pojawia się refleksja: czy ten świat był taki mały czy też bardzo oni starali się o utrzymanie kontaktów długo przed nadejściem Internetu?
Rozwiązanie rachunkowe rzadko jest przedstawiane. Znam jedno, które pochodzi z roku 1994. Autorem artykułu w lutowym wydaniu Mathematics Magazine (mającego tytuł "An Advanced Calculus Approach to Finding the Fermat Point") jest Mowaffaq Hajja. Zazwyczaj rozwiązuje się problem geometrycznie.
Zręczny pomysł użyty w poniższej konstrukcji geometrycznej powinien cię przekonać, że nie ma konfliktu między „estetyczną atrakcyjnością” czyli „miłymi kształtami” a „prostym lecz wydajnym rozumowaniem”.
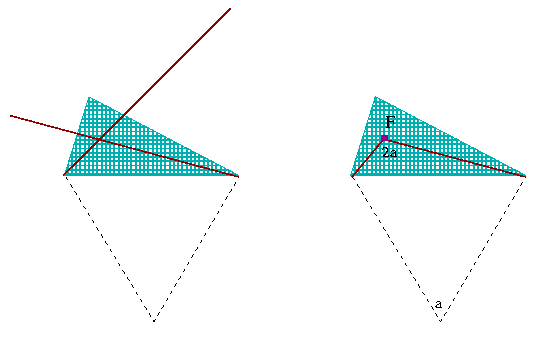
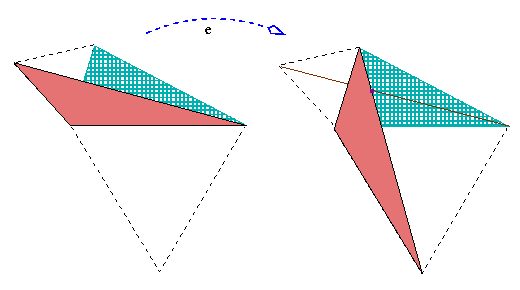
Jeśli wybrać jakikolwiek punkt wewnątrz trójkąta, suma trzech odległości jest taka jak długość łamanej, mającej te same punkty końcowe co i przekątna.
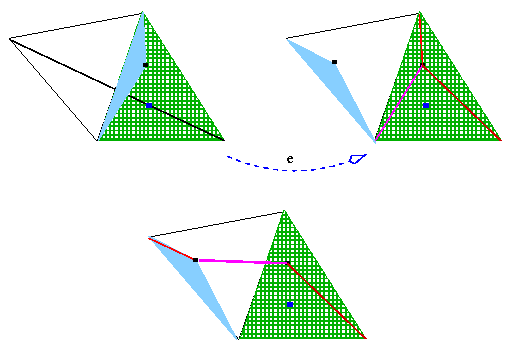
No właśnie, jeśli wziąć punkt Fermata to łamana wyprostowuje się!
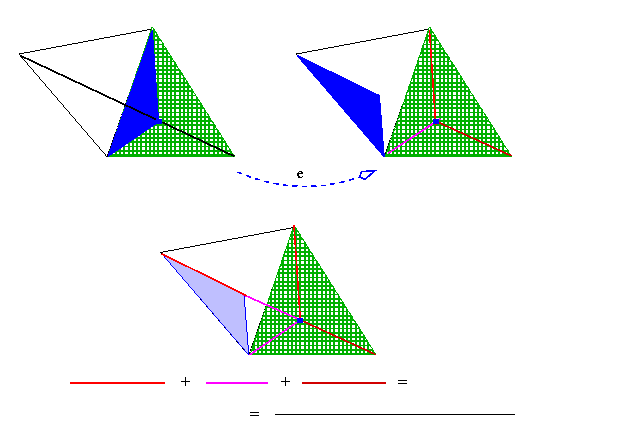
A więc ten wybór daje najmniejszą możliwą sumę odległości.
A w dodatku widzisz, że którakolwiek z trzech przekątnych nadaje się do tej konstrukcji - więc wszystkie trzy przekątne mają tę samą długość!
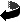 matematyka
matematyka
