The Fermat Point of a Triangle
Se você prefere estórias resumidas, dê uma olhada na pág.83 de Geometry Revisited de H.S.M.Coxeter e S.L.Greitzer.
 |
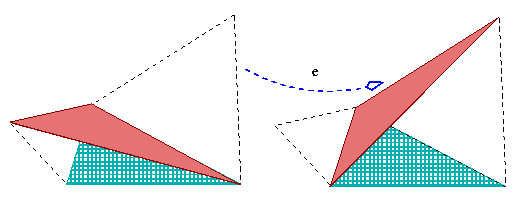
Você recorda-se da canção de Pete Seeger “Se eu tivesse um triângulo”? Bem, suponha que você o tem e você decide colar algumas formas aprazíveis aos lados dele. |
| Se usasse quadrados o desenho seria agradável mas esta vez você não está a fim de lidar de novo com o teorema de Pitágoras ou dos cossenos. Você quer descobrir novas terras. Então porque não usar os triângulos equiláteros? |
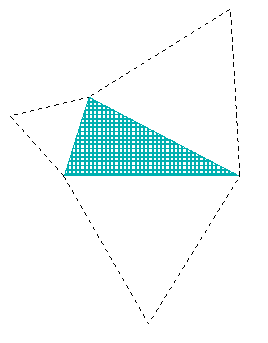
|
|
Parece que se abrem como as pétalas de uma flor. E cada um deles
forma um quadrilátero junto com o triângulo inicial. Isso leva
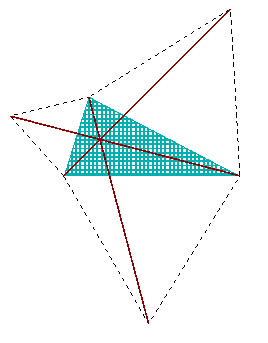
a uma idéia: como isso ficaria se a gente esboçasse as diagonais?
(Você estava esperando que iria falar do teorema de Napoleão? Não, prefiro me ocupar de diagonais esta vez. De fato, o esboço inicial seria o mesmo - mas as estórias são diferentes. |
Será que o traçado é grosso demais ou as diagonais de fato encontram-se em um ponto? Mesmo se conferir esse fato pode levar um tempinho, a tentativa pode ser atraente.
Mas surge uma suspeita. O suposto ponto de cruzamento sempre ficaria dentro do triângulo? Um pouco de experimentos com lápis e compasso mostra que ele poderia fazer um passeio para fora. Deve ser claro que o esboço muda completamente se um dos ângulos alcança 120°.
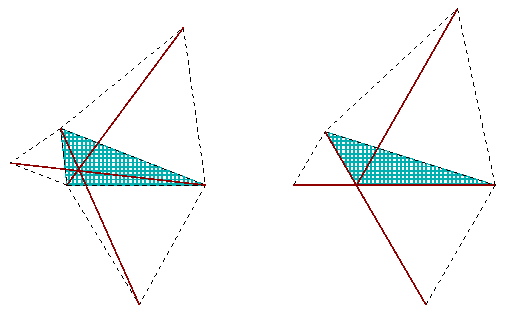
É bom ficar cada vez com uma coisa só. Enquanto questiona-se esse ponto de cruzamento, a análise estaria facilitada se ele se encaixasse dentro do triângulo. Portanto aceite, por favor, que afastamos da nossa análise os triângulos com ângulo que mede 120° ou mais.
| Agora os ângulos de 60° e 90° vão entrar no palco. (Você os chama de Pi/3 e Pi/2? Eu também.) Tendo uns nomes mais curtos para eles pode-se economizar tempo. Permita denotá-los com letras e e r (simplesmente para “igual” e “reto”). E por enquanto remova uma das pétalas. Diga-me, isso não está ficando científico mesmo? | 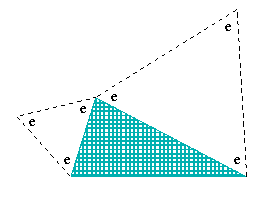 |
Então, o ângulo é e:
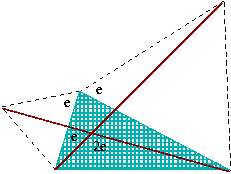 - o mesmo que há em pétalas.
- o mesmo que há em pétalas.
Isso deve parecer conhecido:
De fato, é uma consequência da reversão do teorema sobre o ângulo central (apoiado em uma corda). Concluimos que ambas as circunferências ao redor dos triângulos equiláteros captam também F, o ponto de encontro das duas diagonais.
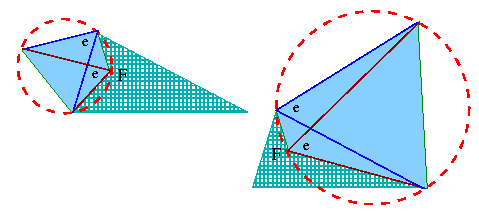
Estaria na hora de chamar no palco a terceira diagonal? Só um momento, há aqui algo mais que você já sabe:
| Tem-se aqui mais um quadrilátero com vértice F que apoia todos os seus vértices em uma circunferência! (O nome técnico para tal figura polinomial é “cíclica”.) Relembre dessa simples condição: a soma dos ângulos opostos do quadrilátero tem que dar 2r. Seria um novo teorema? Nem tanto, isso é mais uma outra consequência do teorema sobre o ângulo central. Então verifique que 2a + a = 2r para ganhar certeza que é possível esboçar mais uma circunferência: |
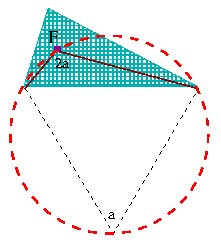
|
Agora sim, vem o ânuglo entre a primeira e a terceira diagonal. Mais um giro, por favor! Mas esta vez no sentido horário.
| O novo ponto de encontro fica também na circunferência ao redor do terceiro triângulo equilátero. Uma circunferência não pode cortar uma linha reta (a diagonal) mais de duas vezes. E já temos dois pontos de intersecção! Um é F é o outro é aquele vértice do triângulo que fica na sua aresta à direita. | 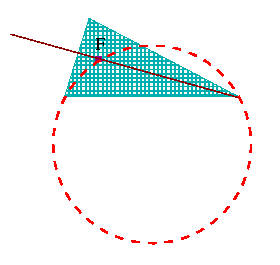 |
| Ótimo. O novo ponto de encontro não se situa na aresta (pois concordamos que os ângulos não alcançarão 120°, certo?), então ele tem que coincidir com F. Chegamos ao ponto que quisemos atingir: todas as três diagonais encontram-se em F, cada par delas formando o ângulo 2a. | 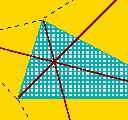 |
Um ponto tão destacado merece um nome distinto - de fato F é chamado de ponto de Fermat do triângulo inicial. |
Isso chama atenção da gente que nele encontram-se as três diagonais, mas para localizá-lo basta ter uma delas e uma das circunferências que circunscrevem as pétalas:
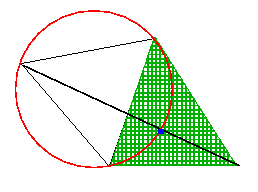
E qual é a justificativa da escolha do seu nome? Bem, há 370 anos
Pierre Fermat fez esta pergunta:
para qual ponto no triângulo com ângulos agudos a soma
de distâncias dos vértices será a menor possível?
Pelo menos assim maioria das fontes coloca a questão. Mas os materiais encontrados na Internet divergem em detalhes. A informação em enciclopédia de Eric Weisstein que diz:
O problema [...] foi proposto pelo Fermat a Torricelli. A solução de Torricelli foi publicada por seu aluno Viviani em 1659
pode ser até correta mas o que foi mesmo que Fermat escreveu? Para mim, mais informativa é esta passagem na contribuição de Harold W. Kuhn. Ele escreve que o desafio de Fermat foi este:
“Dados três pontos no plano, ache o quarto ponto tal que a soma das distâncias até três dados pontos atinge o mínimo!”
Mais tarde aparecerá aqui uma curta estória sobre um resultado de Vicenzo Viviane. Mas porque cito todos esses nomes e conexões? Fermat desafia Toricelli (que era um assistente de Galileo por um curto período), o seu aluno era Viviane - e daí? Bem, a gente vê que todos eles se conheciam e a gente pensa: será que o mundo era tão pequeno ou que eles faziam tudo possível para ter contato, muito antes do advento da Internet?
Raramente apresenta-se uma solução calculacional do problema. Conheço uma, publicada em fevereiro de 1994 no artigo de Mowaffaq Hajja, em Mathematics Magazine. O nome do artigo é “An Advanced Calculus Approach to Finding the Fermat Point”. Costumariamente resolve-se o problema por meio de geometria.
Uma idéia engenhosa usada na construção apresentada abaixo deve convencer que “charme estético” ou “uma forma aprazível” pode combinar bem com “raciocínio simples e eficiente”.
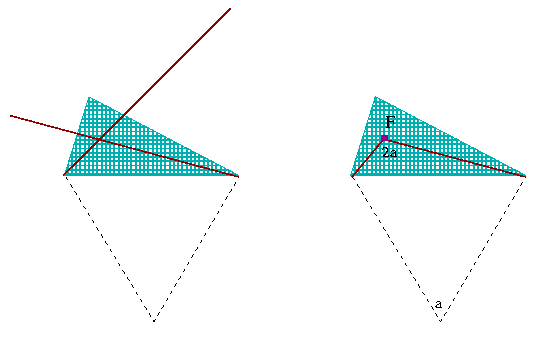
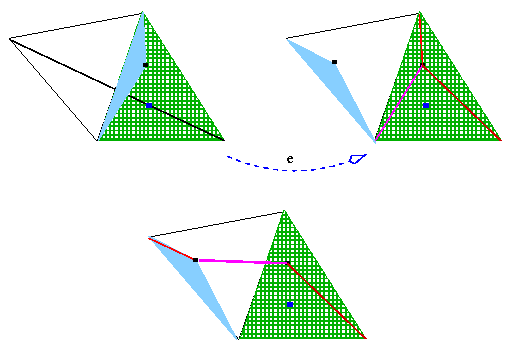
Se escolher um ponto qualquer dentro do triângulo, a soma de três distâncias é a mesma que o comprimento da linha quebrada que compartilha as extremidades com a diagonal.
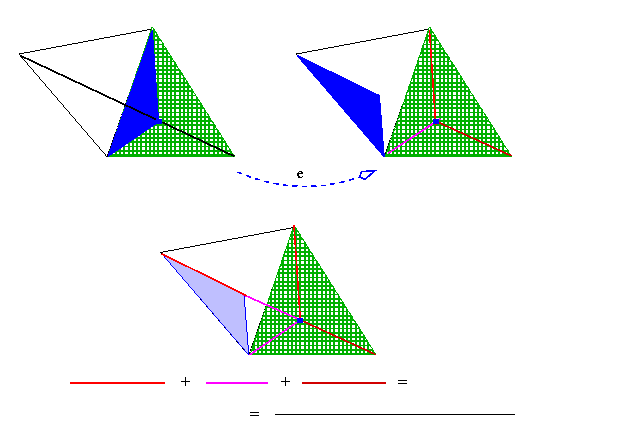
Bem, se escolhe-se o ponto de Fermat, a linha quebrada fica retificada!
Portanto, esta é a escolha que fornece a menor soma possível.
Además, pode-se ver que qualquer das três diagonais poderia ser usada nesta construção - e isso significa que todas elas têm o mesmo comprimento!
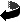 matemática
matemática
