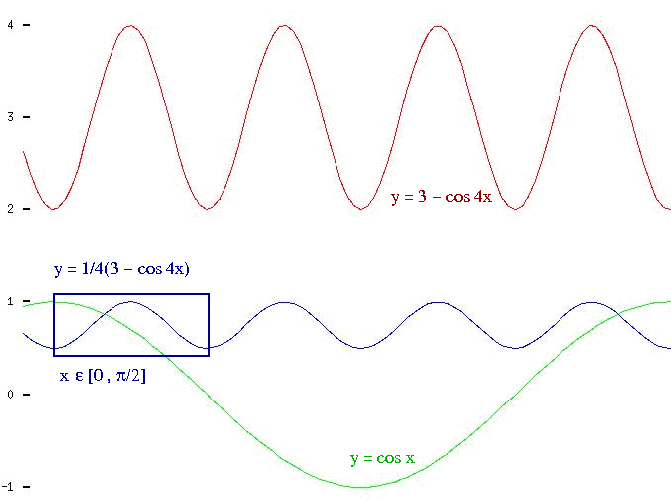
The excercises solved below have been taken from some calculus textbooks. If the books came from a cave of a Crô-Magnon man, they would prove his great mathematical acumen. Alas, they come from a university library.

Examine the function f(x)=cos⁴x + sin⁴x .

Well, let us examine it:

cos⁴x + sin⁴x =
= (cos²x + sin²x)² - 2(cos²x)(sin²x) =
= 1 - (1/2)[2(cos x)(sin x)]² =
= 4/4 - 1/4(2cos²2x) =
= 3/4 - 1/4[2(cos²2x) - 1] =
= 1/4(3 - cos4x) .

The function, carefully examined, lies in the blue box.

Examine the function f(x)=1/(1 +x²) .

The full “examination” is presented in this sketch:

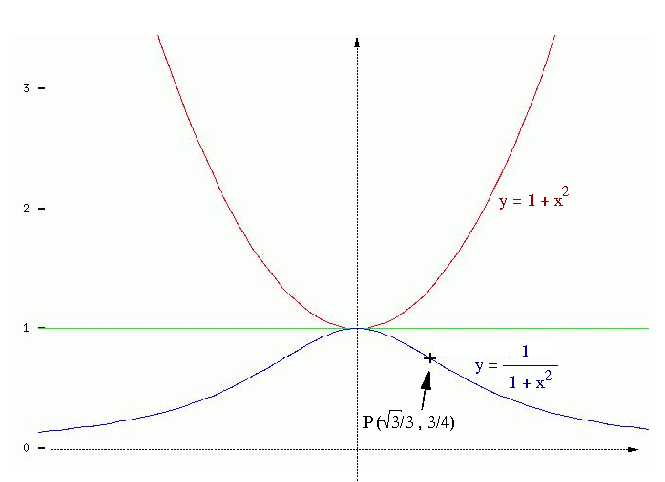
The only information that is actually contributed by the differential calculus refers to the coordinates of the inflection point P (tangent line to the curve crosses to its “other side”). In fact, I would not know how to find them in an elementary way. But using enormous calculus machine to get the other conclusions is…

Examine the function h(x)=(8x + 19)/(2x + 3) .

Even if a high school student did not know the construction of hyperbola, he might start with f(x)=x and obtain the graph of g(x)=1/x. He will notice that f(x) is an odd function, and so is g(x). Therefore if one knowns it for x>0, one knows its entire graph.

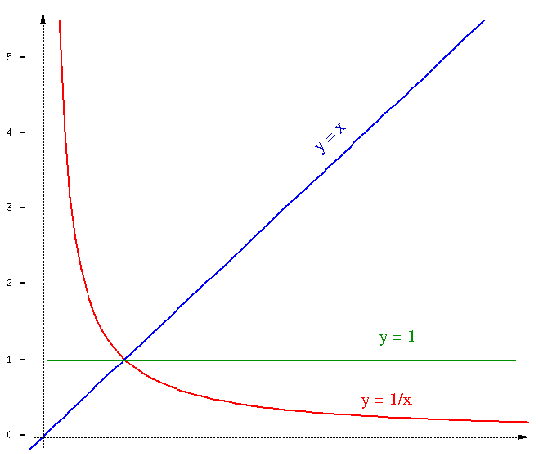
Obviously, the red graph must be symmetric with respect to the straight line with equation y=x, because the function inverse to g(x) has the same form as g(x),

x = g^-1(y) = 1/y .

Transforming h(x) in order to get

h(x) = 4 + 7/(2x + 3) = 4 + 7/2[1/(x + 3/2)]

and tracing the series of sketches for consecutive functions

1/x , 1/(x + 3/2) , 7/2[1/(x + 3/2)] , h(x) we get the result.

Generally speaking, it is worth to invest once in a while in understanding how composing y=f(x) with a linear function modifies f – and then collect profits from the investment for the rest of your life.

All you need to do is to consider four modifications obtained with the help of real numbers b (with separate cases for b>0 and b<0) and a (taking care of three cases: a=-1, 0<a<1, 1<a), that lead from y=f(x) to

(x-->x+b) y=f(x+b)
(y-->y+b) y+b=f(x)
(x-->ax) y=f(ax)
(y-->ay) ay=f(x)

Find the angle that the tangent to the function y=ax² in point (p,ap²) forms with the x axis.

Once upon a time high school students knew the theorem that taking tangent line that passes through (p,ap²), the subtangent to parabola (the segment from 0 to the meeting point of the tangent with the x axix) measures p/2. Take a segment connecting the focus with a point in the directrix, cut it with its perpendicular bisector, reach the bisector by a line from the point in directrix and perpendicular to it (the meeting point belongs to the parabola) and note the the bisector divides the (blue) triangle into two congruent rectangular ones:

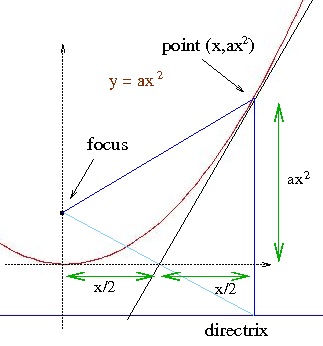
Later take the value of the function inverse to the tangent at (ap²)/(p/2)=2ap and wonder: why should one use derivates here?

Calculate the integral of the function sin²x in the interval from 0 to 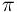/2.

First we trace the graphs of sin²x and cos²x in the rectangle having the base of length 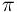/2 and height 1. Then give the sketch a half-turn around the point with coordinates (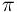/4,1/2) and see that the area that we are looking for is half that of the rectangle.

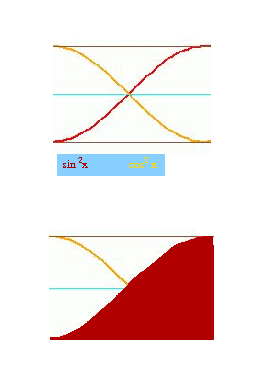
Yes, Pythagorean theorem: sin²x + cos²x = 1 is much older than the integral calculus.

Is it possible to find an elementary way to measure the area between the x axis and the graph of the function 1 - cos x for the interval from 0 to ?

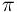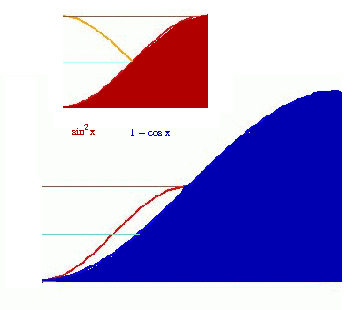
Using trigonometric functions, how to express the conviction that contracting by half horizontally and vertically the graph of the function 1 - cos x we shall get sin²x ?

A Counter-ad of Calculus