Antyreklama analizy matematycznej

Rozwiązane poniżej ćwiczenia są z paru podręczników rachunku różniczkowego i całkowego. Gdyby te książki pochodziły z jakiejś jaskini człowieka z Crô-Magnon, byłyby dowodem jego wielkiej wiedzy matematycznej. Niestety są z biblioteki uniwersyteckiej.

Zbadaj funkcję f(x)=cos⁴x + sin⁴x .

Cóż, badajmy:

cos⁴x + sin⁴x =
= (cos²x + sin²x)² - 2(cos²x)(sin²x) =
= 1 - (1/2)[2(cos x)(sin x)]² =
= 4/4 - 1/4(2cos²2x) =
= 3/4 - 1/4[2(cos²2x) - 1] =
= 1/4(3 - cos4x) .

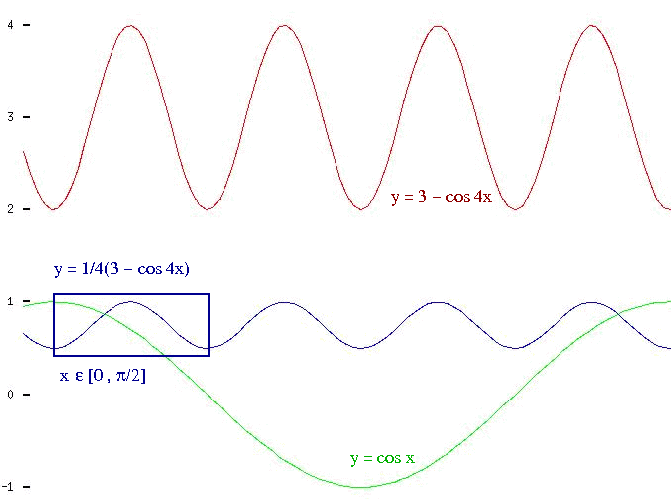
Funkcja, starannie zbadana, leży w niebieskim pudełeczku.

Zbadaj funkcję f(x)=1/(1 +x²) .

Całe „badanie” przedstawia ten szkic:

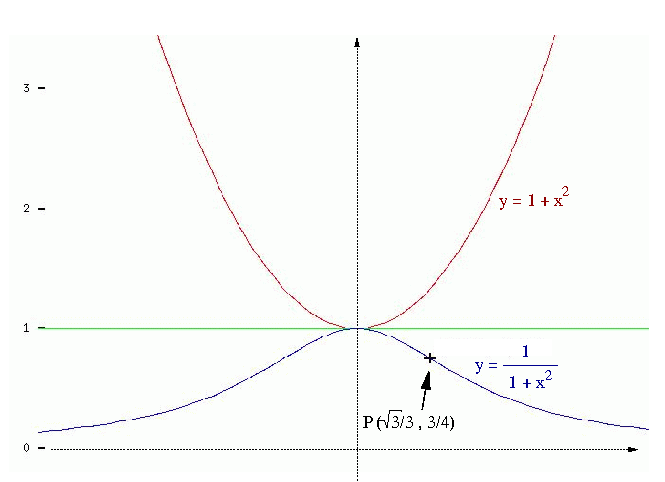
Jedyna informacja, ktorą wychwytuje rachunek różniczkowy to pozycja punktu przegięcia P (w tym punkcie styczna do krzywej przechodzi na jej „drugą stronę”). W istocie nie widzę jak znaleźć współrzędne tego punktu w elementarny sposób. Ale żeby dla reszty wprowadzać olbrzymią maszynerię rachunku różniczkowego…

Zbadaj funkcję h(x)=(8x + 19)/(2x + 3) .

Nawet jeśli uczeń szkoły średniej nie zna konstrukcji hiperboli, potrafi zaczynając od f(x)=x dotrzeć do wykresu g(x)=1/x. Zauważy, że f(x) jest nieparzysta, więc także g(x) jest nieparzysta i znajdując jej wykres tylko dla x>0 potrafimy naszkicować ją całą.

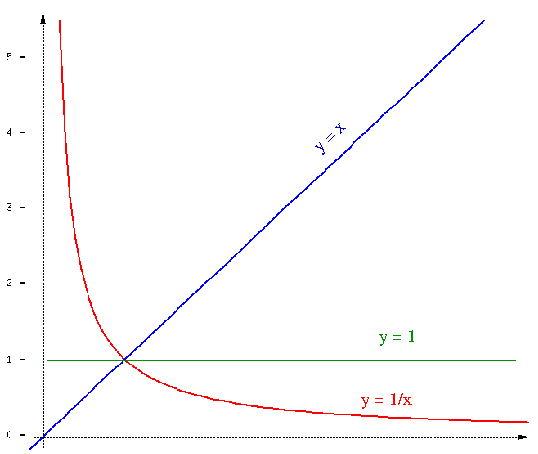
Oczywiście czerwony wykres musi być symetryczny względem prostej o równaniu y=x, bo funkcja odwrotna do g(x) ma tę samą postać co g(x),

x = g^-1(y) = 1/y .

Po przekształceniu h(x) do postaci

h(x) = 4 + 7/(2x + 3) = 4 + 7/2[1/(x + 3/2)]

seria szkiców dla kolejnych funcji:

1/x , 1/(x + 3/2) , 7/2[1/(x + 3/2)] , h(x) kończy dzieło.

Ogólnie mówiąc, warto raz zainwestować w przemyślenie jak złożenie z funkcją liniową modyfikuje y=f(x), by przez resztę życia czerpać stąd zyski.

Wystarczy zastanowić się nad czterema modyfikacjami, przy użyciu liczb rzeczywistych b (osobne przypadki dla b>0 i b<0) oraz a (rozbijając na trzy przypadki: a=-1, 0<a<1, 1<a), prowadzącymi od y=f(x) do

(x-->x+b) y=f(x+b)
(y-->y+b) y+b=f(x)
(x-->ax) y=f(ax)
(y-->ay) ay=f(x)

Znajdź kąt, który styczna do wykresu funkcji y=ax² w punkcie (p,ap²) tworzy z osią x-ów.

Kiedyś uczniowie szkoły średniej znali twierdzenie, że jeśli bierzemy styczną w punkcie (p,ap²) to podstyczna do paraboli (odcinek od 0 do przecięcia się stycznej z osią x-ów) mierzy p/2. Trzeba tylko użyć symetralnej odcinka łączącego ognisko z punktem na kierownicy, poprowadzić od kierownicy prostopadłą aż do symetralnej (to punkt na paraboli) i zauważyć, że symetralna dzieli (niebieski) trójkąt na dwa przystające prostokątne trójkąty:

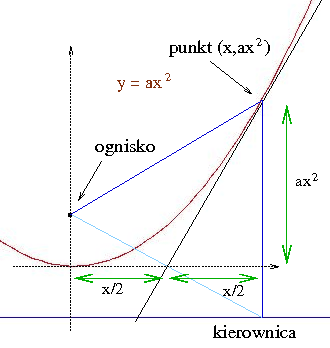
Potem na wartość tangensa: (ap²)/(p/2)= 2ap nakładamy funkcję odwrotną do tangensa i dziwimy się: po co tu pochodna?

Oblicz całkę z funkcji sin²x w przedziale od 0 do 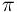/2.

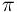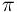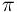Gdy naszkicujemy wykresy sin²x oraz cos²x w prostokącie mającym podstawę o długości /2 oraz wysokość 1, obróciwszy szkic o /2 wokół punktu o współrzędnych (/4,1/2) widać, że poszukiwane pole zajmuje połowę prostokąta.

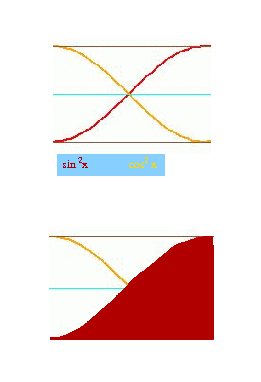
Tak, twierdzenie Pitagorasa: sin²x + cos²x = 1 znacznie wyprzedza rachunek całkowy.

To może także pole między osią x-ów a wykresem funcji 1 - cos x w przedziale od 0 do 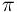można obliczyć w elementarny sposób?

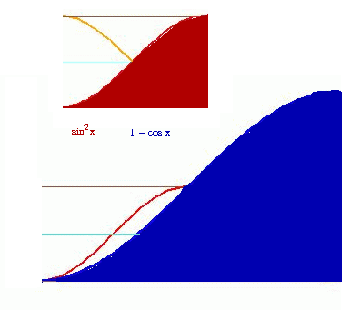
Jak wyrazić w terminach funcji trygonometrycznych przekonanie, że skurczywszy dwukrotnie w pionie i w poziomie wykres funcji 1 - cos x otrzymamy sin²x?