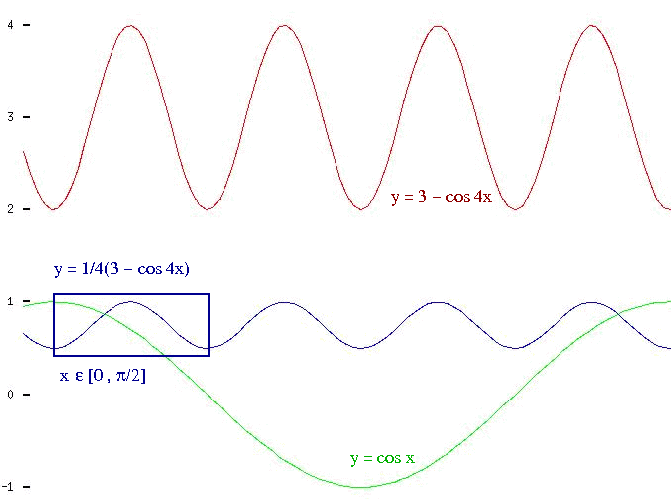
Uma anti-publicidade de análise matemática

Os exercícios resolvidos aqui provêm de alguns livros-textos de Cálculo diferencial e integral. Se estes livros viessem de uma caverna de homem de Crô-Magnon, provariam a sua grande sabedoria em matemática. Infelizmente eles vêm de uma biblioteca universitária.

Examine a função f(x)=cos⁴x + sen⁴x .

Bem, vamos examinar:

cos⁴x + sen⁴x =
= (cos²x + sen²x)² - 2(cos²x)(sen²x) =
= 1 - (1/2)[2(cos x)(sen x)]² =
= 4/4 - 1/4(2cos²2x) =
= 3/4 - 1/4[2(cos²2x) - 1] =
= 1/4(3 - cos4x) .

A função, examinada cuidadosamente, fica em caixinha azul.

Examine a função f(x)=1/(1 +x²) .

A “examinação” inteira está revelada neste esboço:

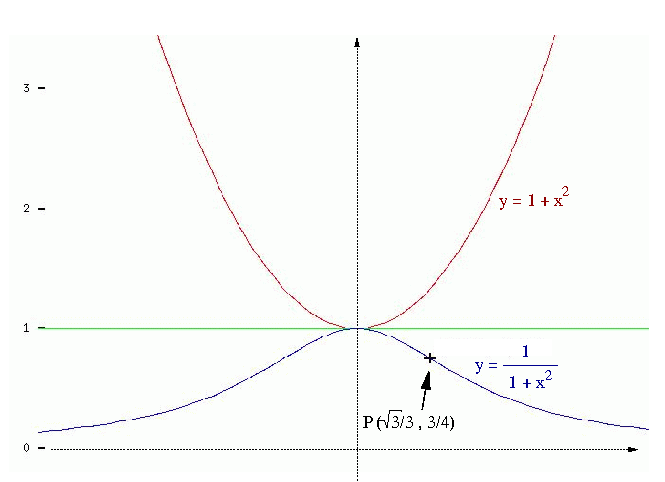
A única informação fornecida pelo cálculo diferencial refere-se à posição do ponto de inflexão P (e nele a tangente à curva passa para o seu “outro lado”). De fato, não vejo como achar coordenadas deste ponto em uma maneira elementar. Mas introduzir a enorme máquina do cálculo diferencial para obter o resto de resultados…

Examine a função h(x)=(8x + 19)/(2x + 3) .

Mesmo se um aluno do segundo grau não conhece a construção da hipérbole, começando com f(x)=x conseguiria chegar ao gráfico de g(x)=1/x. Ele notará que f(x) é ímpar, portanto também g(x) é ímpar –. Assim basta ter seu gráfico só para x>0 para conhecer o gráfico inteiro.

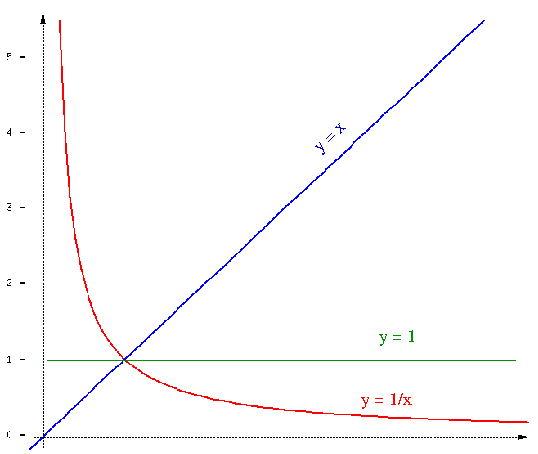
Claramente o esboço vermelho tem de ser simétrico com respeito à reta com equação y=x, pois a função inversa a g(x) tem a mesma forma que g(x),

x = g^-1(y) = 1/y .

Transformando h(x) para obter

h(x) = 4 + 7/(2x + 3) = 4 + 7/2[1/(x + 3/2)]

é suficiente fazer uma série de esboços das funções consecutivas:

1/x , 1/(x + 3/2) , 7/2[1/(x + 3/2)] , h(x) para terminar o trabalho.

Falando em termos gerais, vale a pena investir uma única vez em reflexão como y=f(x) fica modificada em composição com a função linear para ter proveito deste investimento pelo resto da vida.

É suficiente considerar quatro modificações, usando os números reais b (há casos separados para b>0 e para b<0) e a (quebrando isso em três casos: a=-1, 0<a<1, 1<a); elas levam de y=f(x) até

(x-->x+b) y=f(x+b)
(y-->y+b) y+b=f(x)
(x-->ax) y=f(ax)
(y-->ay) ay=f(x)

Ache o ângulo que a reta tangente a y=ax² em ponto (p,ap²) forma com eixo x.

Havia tempos que os alunos da escola de segundo grau conheciam o teorema seguinte: tome a reta tangente em ponto (p,ap²), a subtangente da parábola (o intervalo de 0 até o ponto de contato da tangente com o eixo x) mede p/2. É preciso usar a mediatriz do intervalo que une o foco com um ponto da diretriz, conduzir deste ponto uma perpendicular até a mediatriz (o ponto de encontro fica na parábola) e notar que a mediatriz divide o triângulo (azul) em dois triângulos retângulos congruentes:

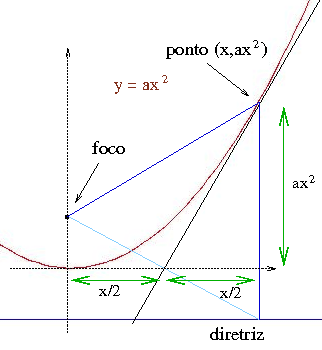
Depois pegamos o valor da função inversa da função tangente para (ap²)/(p/2)= 2ap e estranhamos: para que usar aqui as derivadas?

Calcule a integral da função sen²x no intervalo de 0 até 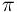/2.

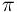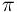Esboçamos os gráficos de funções sen²x e cos²x no retângulo com base de comprimento /2 e com altura 1; depois dando meia-volta ao redor do ponto com coordenadas (/4,1/2) notamos que a figura examinada ocupa a metade da área do retângulo.

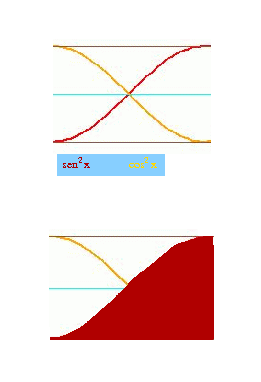
Sim, o teorema de Pitágoras: sen²x + cos²x = 1 é muito mais antigo do cálculo integral.

Ai vem a idéia: talvez a região entre o eixo x e o gráfico da função 1 - cos x no intervalo de 0 até 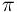possa ser medida?

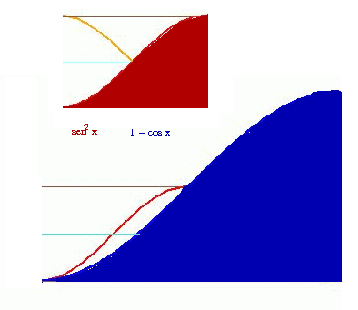
Como expressar em termos de funções trigonométricas a convicção que contraindo pela metade o gráfico da função 1 - cos x tanto no sentido horizontal quanto no vertical obteremos sen²x ?