An advertisment of Calculus

I wonder what advertising agency would try to assist a producer that insists that his product has to keep its brand name “Grass-In-Cow-Out Cheese”. That is the charm which mathematical names carry. It makes you think that mathematician is a wolf to mathematics. But the theory is beautiful and there are lots of students who have to take a course in Calculus. Their studies would be easier if they really liked the topic called Mathematical Analysis or Differential and Integral Calculus.

The best reasons to study it are in physics. It might interest you what the Russian mathematician V.I.Arnold has to say: “Mathematics is a part of physics.”. But if you need motives that are simple and easy to understand, think of measuring the arcs of curves and areas contained between them.

Archimedes would recognize this form

One of masterpieces of our civilization is Archimedes' calculation that he used to find the area of the region between a parabola and its chord. Some historians think that his ideas have lead much later to some notions of Calculus and to infinite sums for geometric sequence. The language used to present those calculations has been enormously simplified during more than 2200 years that separate us from Archimedes. Still, a walk along the path his reasoning indicates asks for more patients and dedication for maths that most of today's student have.

Let me recall that “parabola” meant just parabola to Archimedesa (choose a line in the plane and then a point outside the line; give the name of parabola to the set of those points of the plane that have the same distance from both chosen objects) and not a “graph of a second degree equation”. The last expression would not make sense to him (a link between geometrical objects and algebraic description appeared 1900 years later). And it does not make sense today, although it is frequently used by teachers who do not really care about their students. And it should be so obvious: if someone asks: “who was Newton?”, can we accept the answer: “he was the man whose first name is spelled i-s-double a-c”?.

When you get the diploma of high school probably you do not expect to see any more parabolas cutting the axes x and y, but the meeting of two parabolas will bring nicer impression:

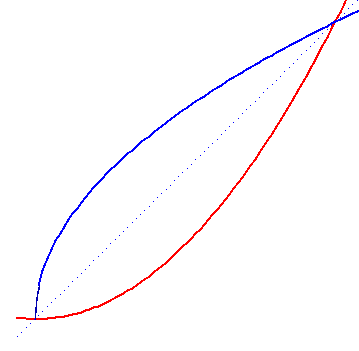
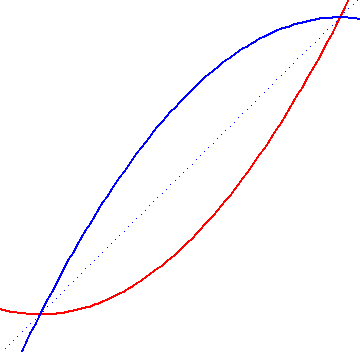
If the coordinates are chosen so that the curves of the first sketch are described by equations

y = x² and x = y²
than it should not be terribly difficult to invent the description of curves of the second one. And if you know how to get its shape making folds on a sheet of tracing paper and you realize that the folds are lines tangent to the parabola, you may even find out the angles at which the curves meet.

But the challenge to find the area between the curves either turns one back to cumbersome techniques from the antiquity or it calls for the application of integral calculus. And it comes as a nice surprise that all the three figures in this square

have the same area.

There are leaves like that

Lower the “red” parabola by 1, shift by 1 to the left the “blue” one – the description did not become much more difficult but the obtained form became more interesting. Sorry, I do not know botanical taxonomy, so I will not quote the Latin name of the tree (would you help me out here?) but I have already met leaves with precisely this type of cut.

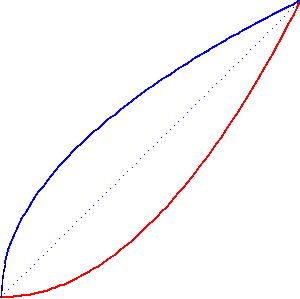
High school knowledge suffices to find coordinates of four meeting points of the curves.

Two of them: (-1,0) and (0,-1) are obvious enough. Still, two other ones are expressed by the numb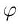er (golden mean!) and its inverse; a nice encounter. Besides, the length of the segment contained in the symmetry axis is the square root of 10, the number giving an excellent approximation (with error smaller than 1%) of another famous number, stemming out from a very different figure, the number .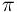

Elementary considerations show that the four points lie on the circle that circunscribes the leaf. The equation of the circle is

(x-1)² + (y-1)² = 5/2

It is equally simple to find out that the circle with equation

x² + y² = 3/4

is inscribed in the leaf (touches all its four borders). The distance of the latter circle to the closer of its two “sharp” points is

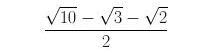
– it can be substituted by rational number 5^-3 commiting an error smaller than 10^-5 .

The number is so small that – making the design of correct proportions – we could visualize it only if the sketch were spread out on a table. The alternative is an approach of an artist who stresses the essential and manages to deform and make inconspicuous the rest. Luck has it that a friend of mine, Jurek Kocik, is a mathematician as well as an artist and has a knack for performing such tricks. That is how he rendered it (and I render him my hommage because I would not know to produce such a simple design):

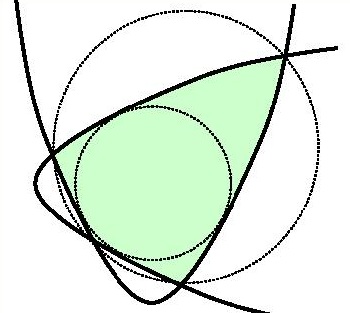
So, we have many nice results at a low calculational expense – but it does not seem easy to discover without integral calculus that the leaf measures 11/3.

The just division

Knowing that Diabostan developed Puf-Puf (the weapons of mass destruction), the leaders of Angeland, helped by the Jawohland, removed the perils by conquest of the whole Diabostan. Hence, there appeared the problem of just and honest division of the land of their enemies along the line of some latitude. As the Jawohland covered 20% of the costs of the war effort, it should get 20% of the land, south of that line. That is the map of Diabostan:

Because of curved frontier lines, the solution asks for the use of Integral Calculus. If 90 years ago the frontiers of Diabostan had been traced with straight lines only, the present problem could have been solved at the level of High School geometry.

Four areas

An easy problem: explain why the four figures (contained between the pairs of curves) have the same area.

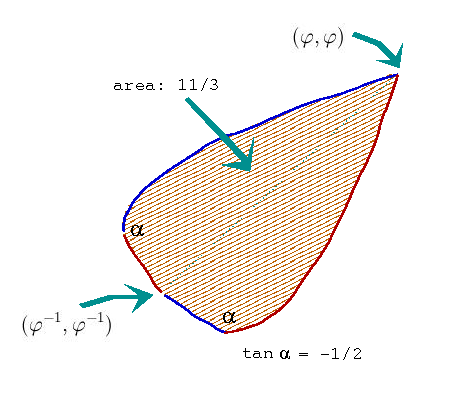
The “common sense” should help to find good line of arguments. But it will not suffice to show tha the area measures 4/3. In order to get the result one has to use the integral calculus – on of the simplest possible applications of that powerful tool.

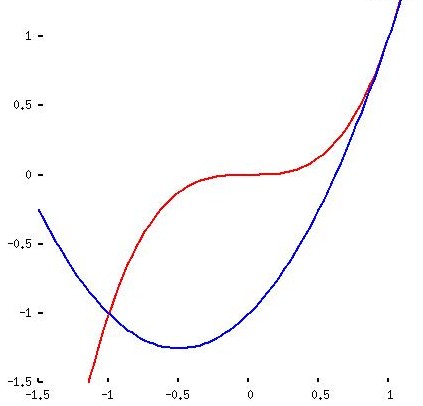
y₁ = x³ y₂ = x² + x - 1	y₁ = x³ - x y₂ = x² - 1
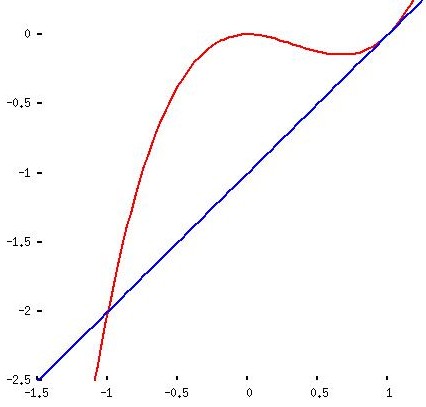
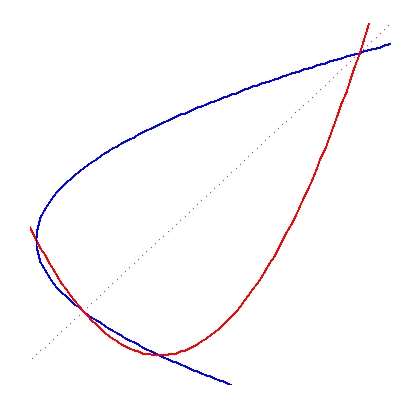
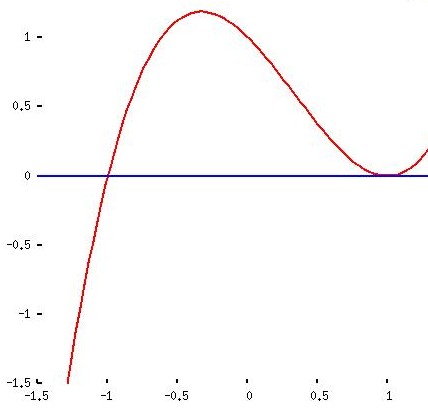
y₁ = x³ - x² y₂ = x - 1	y₁ = x³ - x² - x + 1 y₂ = 0

The said “common sense” (that is: the capacity to apply high school knowledge when solving polynomial equations) is enough to show that the all the pairs of curves meet at horizontal coordinates -1 and 1. But you need th differential calculus to find out that the highest point in the fourth sketch has coordinates (-1/3 , 32/27). This information (sketch a triangle with this vertex and two meeting points mentioned before) leads to conclusion that the number 32/27 gives the area of the triangle and you may visually estimate the size of error when the triangle substitutes the figure.

Here you can take the closer look at the graphs of the functions.