O nome não é atraente, mas a teoria é bela. É também obrigatória para um grande número de estudantes – e a vida deles seria mais fácil se eles gostassem sinceramente da disciplina chamada Análise Matemática, conhecida também sob o codinome de Cálculo Diferencial e Integral.
As motivações mais empolgantes encontram-se na física. (Por sinal, na opinião do matemático russo V.I.Arnold “matemática é uma parte da física”.) Mas outras funcionam mais rápido, pois são mais fáceis de compreender. Elas são ligadas com medição de comprimento de curvas e de áreas de regiões contidas entre as curvas.
Por via de dúvidas vou lembrar que para Arquimedes “parábola” significava justamente parábola (no plano fixe uma reta e um ponto fora dela; chame de parábola o conjunto de pontos do plano equidistantes desses dois objetos) e não um tal de “gráfico de uma equação quadrática”. Esta expressão não faria sentido para ele (uma conexão entre entes geométricos e as suas descrições algébricas ia surgir 1900 anos mais tarde) e continua não fazendo sentido hoje em dia, mesmo sendo usada e abusada pelos educadores que não gostam de seus alunos. Um momento de reflexão basta para resolver se ouvindo a pergunta “quem era Newton?” seria tratada como sensata resposta: “aquele que teve o nome escrito com as letras i-s-a-a-c”.
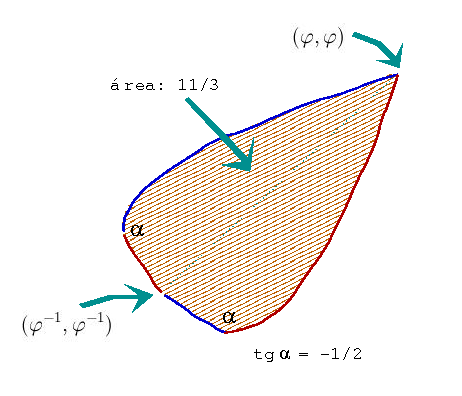
Terminando a escola de segundo grau o aluno está farto de ver as parábolas que cruzam os eixos de coordenadas, mas o encontro de duas parábolas pode ser mais agradável ao seu olho:
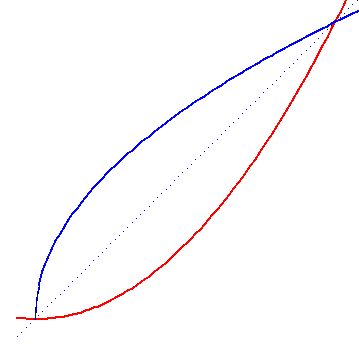
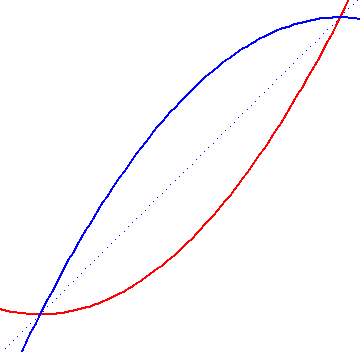
Se o sistema de coordenadas for escolhido assim que as curvas do
primeiro esboço são descritas pelas equações
Mas o cálculo da área da figura por meios elementares seria um
desafio excessivamente difícil. Esta tarefa pede
o uso do Cálculo Integral. Logo vem uma surpesa agradável
que neste quadrado
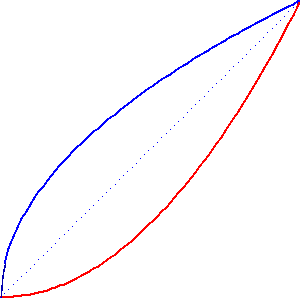
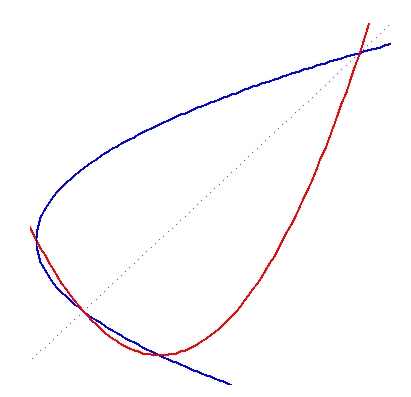
Os conhecimentos da escola são suficientes para obter as coordenadas de quatro pontos de encontros das curvas.
Dois lugares: (-1,0) e (0,-1)
são bastante óbvios. Mas os dois outros envolvem o número
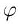(divisão áurea!) e o seu inverso;
um encontro agradável. E ainda o comprimento do intervalo que fica
no eixo da simetria é a raiz quadrada de 10, uma boa aproximação
(com erro abaixo de 1%) do outro número famoso ligado com totalmente
diferente figura, do número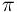 
.
É fácil conferir que esses quatro pontos ficam em uma circunferência
que sobreescreve a folha. A equação da circunferência é
Há um outro fato igualmente fácil: circunferência com equação
está inscrita na folha (toca-a em pontos de suas quatro bordas). A distância desta circunferência até o “ponto final” da folha é
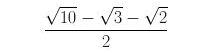
– o número que pode ser substituido pelo número racional 5-3 com erro abaixo de 10-5 .
É um número tão pequeno que para enxergar nitidamente o afastamento das curvas precisaríamos de um esboço do tamanho de toalha de mesa. Um outro jeito é de adotar uma visão artística para destacar o importante e negligenciar resto. É a minha sorte que um amigo meu é tanto matemático quanto artista e com facilidade visualiza as idéias com leves distorções gráficas. Eis como Jurek Kocik resolveu este problema (e o agradeço por isso, pois não saberia achar uma solução tão simples):
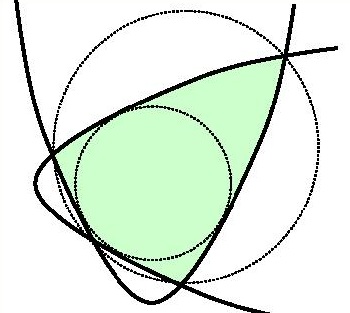
Em soma, temos recebido muitos resultados bonitos sem investir pesadamente em cálculos – mas nenhum caminho fácil leva à descoberta que a folha mede 11/3. Este resultado, sim, segue de uma aplicação simples do Cálculo Integral.
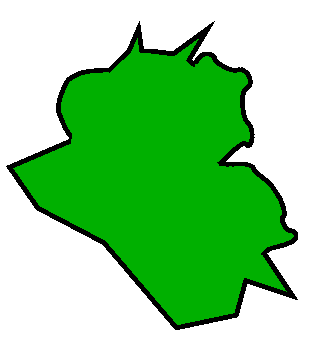
Um tal de “senso comum” ajudará encontrar um bom argumento, mas não servirá sequer um pouco para descobrir que a área é 4/3. Mais uma vez, esta tarefa exige uma simples aplicação da poderosa ferramenta de Cálculo Integral.
 |
 |
 |
 |
|
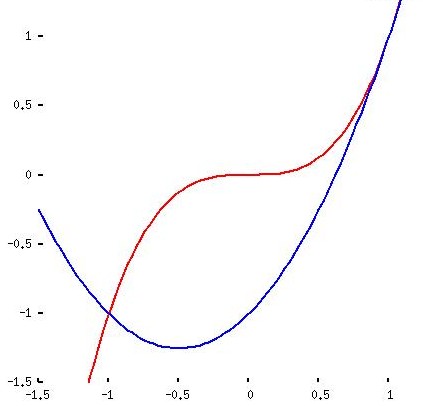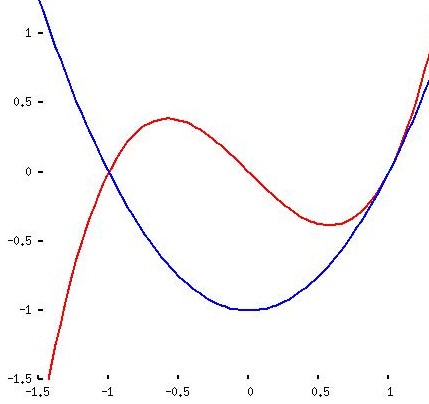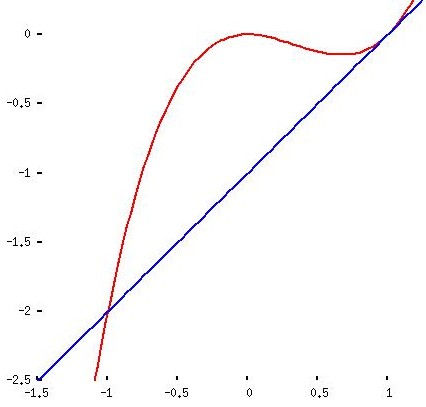
y1 = x3 y2 = x2 + x - 1 |
y1 = x3 - x y2 = x2 - 1 |
|
y1 = x3 - x2 y2 = x - 1 |
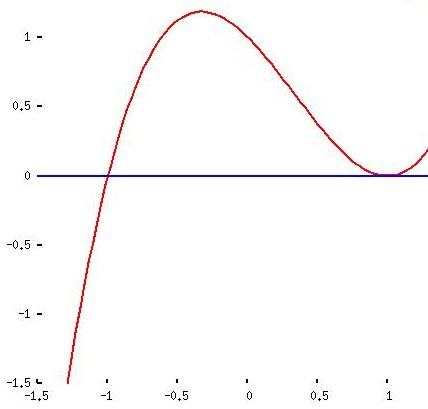
y1 = x3 - x2 - x + 1
y2 = 0 |
Aquele senso comum (isto é: a capacidade de usar os conhecimentos obtidos na escola de segundo grau em questão de equações polinomiais) basta para provar que todos os pares de curvas encontram-se em pontos que têm as coordenadas horizontais -1 e 1. Mas é preciso o Cálculo Diferencial para achar as coordenadas do ponto mais alto no quarto esboço – e elas são (-1/3 , 32/27). Daqui, marcando um triângulo com este vértice e dois outros dados pelos encontros das curvas, chega-se a ver que a área do triângulo é 32/27. O erro cometido na substituição da figura pelo triângulo pode ser avaliado visualmente.
Aqui você pode ver todos os gráficos ampliados.