Najciekawsze motywacje do zajęcia się nią są w fizyce. Tu warto przypomnieć, że w opinii rosyjskiego matematyka V.I.Arnolda „matematyka to część fizyki”. Najszybsze, bo najłatwiejsze do zrozumienia, wiążą się z mierzeniem długości krzywych i pól zawartych między krzywymi.
Na wszelki wypadek przypomnę, że „parabolą” dla Archimedesa była właśnie parabola (ustal na płaszczyźnie linię prostą i punkt nie leżący na niej; nazwij parabolą zbiór punktów płaszczyzny równoodległych od tych dwóch wybranych tworów) a nie jakiś „wykres równania kwadratowego”. To określenie nie miałoby sensu dla niego (powiązanie tworów geometrycznych z opisem algebraicznym miało pojawić się 1900 lat później) – i dziś też nie ma sensu, choć jakże często jest używane przez nauczycieli nielubiących swoich uczniów. Chwilka zastanowienia się wystarczy, by zdecydować czy po usłyszeniu pytania „kim był Kopernik?” ma sens odpowiedzenie: „był człowiekiem, którego imię zapisuje się m-i-k-o-ł-a-j”.
Kończąc szkołę średnią uczeń może być znużony oglądaniem paraboli przecinającej w różnych miejscach osie współrzędnych, ale zetknięcie się dwóch paraboli wywoła chyba milsze doznania estetyczne:
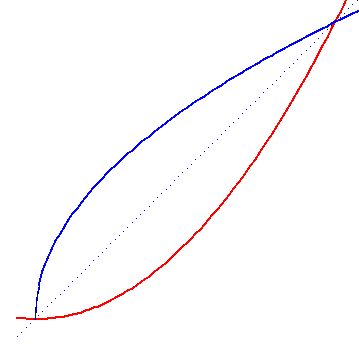
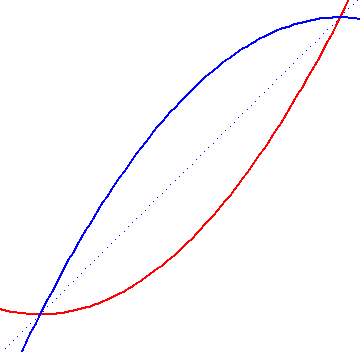
Jeśli tak wybierzemy układ współrzędnych, że w pierwszym szkicu krzywe
będą opisane równaniami
Ale obliczenie pola zawartego między krzywymi, jeśli nie ma znużyć
niemocą większości podejmujących wyzwanie, wymaga użycia rachunku
całkowego i jest miłą niespodzianką, że w tym kwadracie
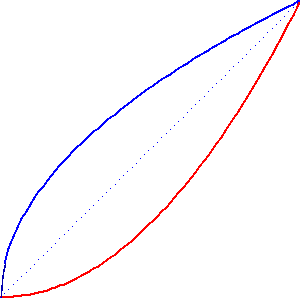
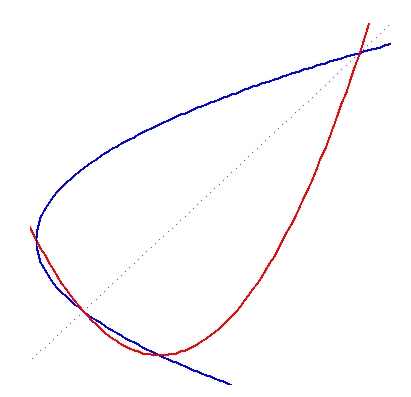
Szkolne umiejętności pozwolą doliczyć się współrzędnych czterech skrzyżowań krzywych.
Dwa miejsca: (-1,0) oraz (0,-1)
nie są niespodzianką. Ale dwa pozostałe wyrażają się poprzez
liczbę 
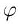(złoty podział!)
i liczbę odwrotną do niej; miłe spotkanie. A w dodatku, długość
odcinka leżącego na osi symetrii to kwadratowy pierwiastek
z 10, liczba wyśmienicie przybliżająca (z błędem poniżej 1%)
inną sławną liczbę, pochodzącą z zupełnie innej figury, liczbę
.
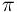Elementarne narzędzia pozwalają ustalić, że te cztery punkty
leżą na okręgu opisanym na listku. Jego równanie to
Równie prosto stwierdza się, że okrąg z równaniem
jest wpisany w listek (styczny z jego czterema brzegami). Odległość tego okręgu od krańcowego a pobliskiego punktu listka to
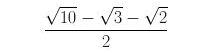
– co można wyrazić liczbą wymierną 5-3 popełniając błąd poniżej 10-5 .
To tak mała liczba, że przy zachowaniu proporcji zobaczymy coś rozkładając rysunek-obrus na stole – albo użyjemy wręcz artystycznego podejścia, by ważne podkreślić a nieważne jakoś zdeformować i w kąt upchnąć. Mam na szczęście przyjaciela, który niezależnie od bycia matematykiem jest też artystą i potrafi robić takie sztuki. Oto jak Jurek Kocik ujął to, co tu istotne (za co jestem mu szczerze wdzięczny, bo nie umiem robić takich prostych szkiców):
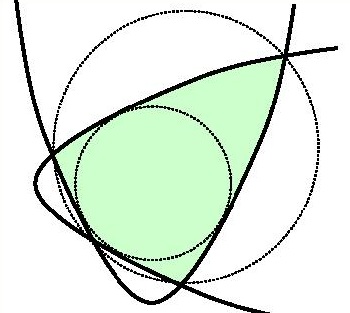
Wiele ładnych rezultatów otrzymanych przy niskim nakładzie rachunków – ale nie wydaje się nic a nic łatwym odkrycie rachunku całkowego, że listek ma miarę 11/3.
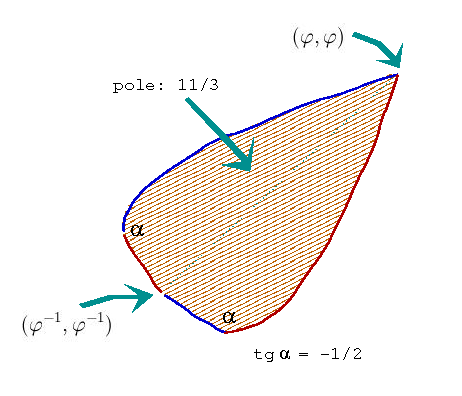
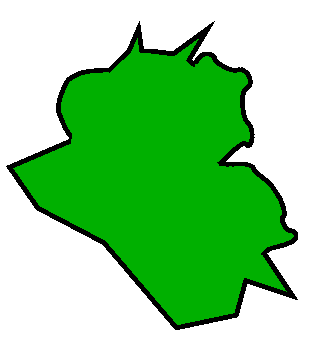
Tzw. „zdrowy rozsądek” pomoże znaleźć dobry argument. Ale nie przyda się on, by dowieść, że to pole mierzy 4/3. Tu trzeba użyć (jeden z najprostszych użytków tego potężnego narzędzia) rachunku całkowego.
 |
 |
 |
 |
|
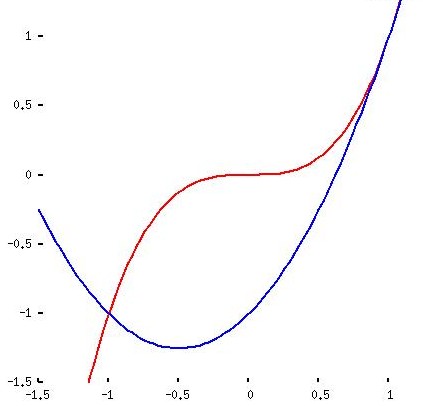
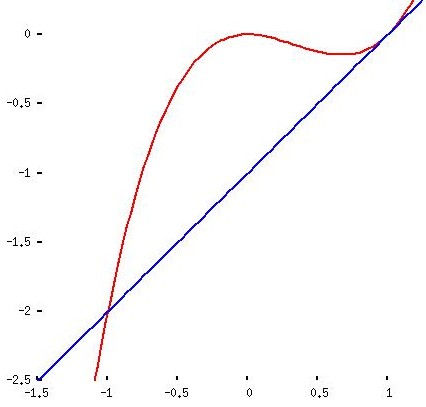
y1 = x3 y2 = x2 + x - 1 |
y1 = x3 - x y2 = x2 - 1 |
|
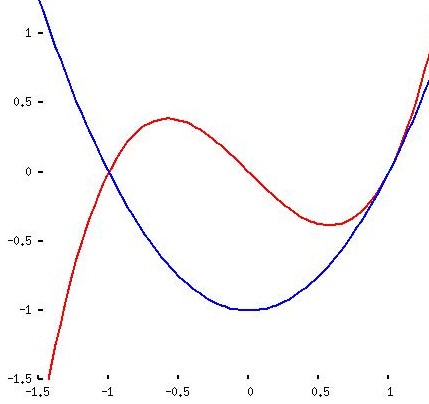
y1 = x3 - x2 y2 = x - 1 |
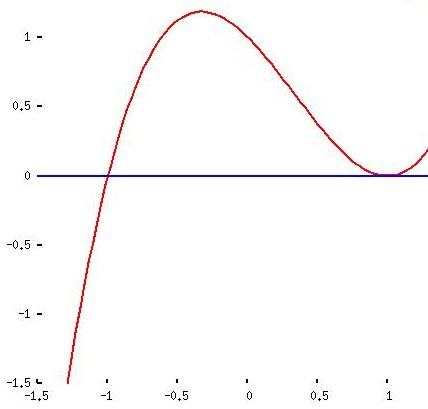
y1 = x3 - x2 - x + 1
y2 = 0 |
Ów zdrowy rozsądek (czyli umiejętność spożytkowania wiedzy ze szkoły średniej dotyczącej rozwiązywania równań wielomianowych) wystarczy, by dowieść, że krzywe spotykają się w punktach mających poziome współrzędne -1 oraz 1. Ale nieodzowny jest rachunek różniczkowy, by odkryć, że najwyższy punkt czwartego wykresu ma współrzędne (-1/3 , 32/27). Ta informacja (nakreśl trójkąt z tym wierzchołkiem i dwoma punktami przecięć krzywych) prowadzi do wniosku, że liczba 32/27 wyraża pole tego trójkąta i można wzrokowo szacować wymiar błędu przy zastąpieniu figury trójkątem.
Tutaj możesz oglądnąć te grafiki w powiększeniu.